题目内容
已知抛物线y=3ax2+2bx+c
(1)若a=b=1,c=-1求该抛物线与x轴的交点坐标;
(2)若a=
,c=2+b且抛物线在-2≤x≤2区间上的最小值是-3,求b的值;
(3)若a+b+c=1,是否存在实数x,使得相应的y的值为1,请说明理由.
(1)若a=b=1,c=-1求该抛物线与x轴的交点坐标;
(2)若a=
| 1 |
| 3 |
(3)若a+b+c=1,是否存在实数x,使得相应的y的值为1,请说明理由.
考点:二次函数综合题
专题:
分析:(1)直接将a=b=1,c=-1代入求出即可;
(2)利用当x=-b<-2时,即b>2,此时-3=(-2)2+2×(-2)b+b+2;当x=-b>2时,即b<-2,则有抛物线在x=2时取最小值为-3,此时-3=22+2×2b+b+2;当-2≤-b≤2时,即-2≤b≤2,则有抛物线在x=-b时,取最小值为-3,分别求出符合题意的答案即可;
(3)由y=1得3ax2+2bx+c=1,则△=4b2-12a(c-1),求出△的符号得出答案即可.
(2)利用当x=-b<-2时,即b>2,此时-3=(-2)2+2×(-2)b+b+2;当x=-b>2时,即b<-2,则有抛物线在x=2时取最小值为-3,此时-3=22+2×2b+b+2;当-2≤-b≤2时,即-2≤b≤2,则有抛物线在x=-b时,取最小值为-3,分别求出符合题意的答案即可;
(3)由y=1得3ax2+2bx+c=1,则△=4b2-12a(c-1),求出△的符号得出答案即可.
解答:解:(1)当a=b=1,c=-1时,抛物线为:y=3x2+2x-1,
∵方程3x2+2x-1=0的两个根为:x1=-1,x2=
.
∴该抛物线与x轴公共点的坐标是:(-1,0)和(
,0);
(2)a=
,c-b=2,则抛物线可化为:y=x2+2bx+b+2,
其对称轴为:x=-b,
当x=-b<-2时,即b>2,则有抛物线在x=-2时取最小值为-3,
此时-3=(-2)2+2×(-2)b+b+2,
解得:b=3,符合题意,
当x=-b>2时,即b<-2,则有抛物线在x=2时取最小值为-3,此时-3=22+2×2b+b+2,
解得:b=-
,不合题意,舍去.
当-2≤-b≤2时,即-2≤b≤2,则有抛物线在x=-b时,取最小值为-3,
此时-3=(-b)2+2×(-b)b+b+2,
化简得:b2-b-5=0,
解得:b1=
(不合题意,舍去),b2=
.
综上:b=3或b=
.
(3)由y=1得3ax2+2bx+c=1,
△=4b2-12a(c-1),
=4b2-12a(-a-b),
=4b2+12ab+12a2,
=4(b2+3ab+3a2),
=4[(b+
a)2+
a2],
∵a≠0,△>0,
所以方程3ax2+2bx+c=1有两个不相等实数根,
即存在两个不同实数x0,使得相应y=1.
∵方程3x2+2x-1=0的两个根为:x1=-1,x2=
| 1 |
| 3 |
∴该抛物线与x轴公共点的坐标是:(-1,0)和(
| 1 |
| 3 |
(2)a=
| 1 |
| 3 |
其对称轴为:x=-b,
当x=-b<-2时,即b>2,则有抛物线在x=-2时取最小值为-3,
此时-3=(-2)2+2×(-2)b+b+2,
解得:b=3,符合题意,
当x=-b>2时,即b<-2,则有抛物线在x=2时取最小值为-3,此时-3=22+2×2b+b+2,
解得:b=-
| 9 |
| 5 |
当-2≤-b≤2时,即-2≤b≤2,则有抛物线在x=-b时,取最小值为-3,
此时-3=(-b)2+2×(-b)b+b+2,
化简得:b2-b-5=0,
解得:b1=
1+
| ||
| 2 |
1-
| ||
| 2 |
综上:b=3或b=
1-
| ||
| 2 |
(3)由y=1得3ax2+2bx+c=1,
△=4b2-12a(c-1),
=4b2-12a(-a-b),
=4b2+12ab+12a2,
=4(b2+3ab+3a2),
=4[(b+
| 3 |
| 2 |
| 3 |
| 4 |
∵a≠0,△>0,
所以方程3ax2+2bx+c=1有两个不相等实数根,
即存在两个不同实数x0,使得相应y=1.
点评:此题主要考查了二次函数综合以及根的判别式和一元二次方程的解法等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
下列运算正确的是( )
| A、a•a2=a2 |
| B、a6÷a2=a4 |
| C、(ab)2=ab2 |
| D、(a2)3=a5 |
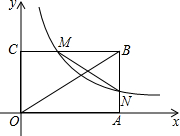 如图,矩形OABC在第一象限,OA,OC分别于x轴,y轴重合,面积为6.矩形与双曲线y=
如图,矩形OABC在第一象限,OA,OC分别于x轴,y轴重合,面积为6.矩形与双曲线y= 在△ABC中,AB=AC,D为BC的中点,四边形ABDE是平行四边形.
在△ABC中,AB=AC,D为BC的中点,四边形ABDE是平行四边形. 如图,已知?ABCD中,∠ABC的平分线BE交CD于点E,过点E作EG∥BC交AB于点G,试判断四边形BCEG的形状,并说明理由.
如图,已知?ABCD中,∠ABC的平分线BE交CD于点E,过点E作EG∥BC交AB于点G,试判断四边形BCEG的形状,并说明理由. 如图,△ABC中,∠ABC的平分线与△ABC的外角∠DAC、∠ACF的平分线相交于点E,EH⊥AC,垂足为点H.求证:∠AEB=∠CEH.
如图,△ABC中,∠ABC的平分线与△ABC的外角∠DAC、∠ACF的平分线相交于点E,EH⊥AC,垂足为点H.求证:∠AEB=∠CEH.