题目内容
13.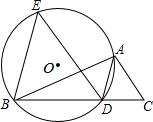 如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点.过点B作BE∥AD,交⊙O于点E,连接ED
如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点.过点B作BE∥AD,交⊙O于点E,连接ED(1)求证:ED∥AC;
(2)若BD=2CD,设△EBD的面积为S1,△ADC的面积为S2,且S12-16S2+4=0,求△ABC的面积.
分析 (1)由AD是△ABC的角平分线,得到∠BAD=∠DAC,由于∠E=∠BAD,等量代换得到∠E=∠DAC,根据平行线的性质和判定即可得到结果;
(2)由BE∥AD,得到∠EBD=∠ADC,由于∠E=∠DAC,得到△EBD∽△ADC,根据相似三角形的性质相似三角形面积的比等于相似比的平方即可得到结果.
解答 (1)证明:∵AD是△ABC的角平分线,
∴∠BAD=∠DAC,
∵∠E=∠BAD,
∴∠E=∠DAC,
∵BE∥AD,
∴∠E=∠EDA,
∴∠EDA=∠DAC,
∴ED∥AC;
(2)解:∵BE∥AD,
∴∠EBD=∠ADC,
∵∠E=∠DAC,
∴△EBD∽△ADC,且相似比k=$\frac{BD}{DC}=2$,
∴$\frac{{S}_{1}}{{S}_{2}}$=k2=4,即s1=4s2,
∵${{s}_{1}}^{2}$-16S2+4=0,
∴16${{S}_{2}}^{2}$-16S2+4=0,
即${({4S}_{2}-2)}^{2}$=0,
∴S2=$\frac{1}{2}$,
∵$\frac{{S}_{△ABC}}{{S}_{2}}$=$\frac{BC}{CD}$=$\frac{BD+CD}{CD}$=$\frac{3CD}{CD}$=3,
∴S△ABC=$\frac{3}{2}$.
点评 本题考查了相似三角形的判定和性质,角平分线的性质,平行线的性质,记住相似三角形面积的比等于相似比的平方是解题的关键.

练习册系列答案
相关题目
3.某班开展1分钟仰卧起坐比赛活动,5名同学的成绩如下(单位:个):37、38、40、40、42.这组数据的众数是( )
| A. | 37 | B. | 38 | C. | 40 | D. | 42 |
4.分式方程$\frac{2}{x-3}$=$\frac{3}{x}$的解为( )
| A. | x=0 | B. | x=3 | C. | x=5 | D. | x=9 |
1.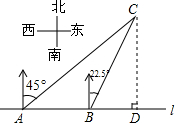 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )| A. | 4km | B. | (2+$\sqrt{2}$)km | C. | 2$\sqrt{2}$km | D. | (4-$\sqrt{2}$)km |
18.下列立体图形中,俯视图是正方形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.若分式$\frac{x-2}{x+1}$的值为0,则x的值为( )
| A. | 2或-1 | B. | 0 | C. | 2 | D. | -1 |
2.若一对邻补角之差是40°,这两个角分别是( )
| A. | 110°,70° | B. | 100°,140° | C. | 100°,60° | D. | 120°,80° |
 如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.