题目内容
2．
如图，矩形ABCD的对角线AC、BD相交于点O，∠AOD=120°，AB=4cm，则矩形的对角线长为8cm．
分析 根据邻补角的定义求出∠AOB=60°，再根据矩形的对角线互相平分且相等可得AO=BO=CO，然后判断出△AOB是等边三角形，根据等边三角形三条边都相等可得AO=AB，然后求解即可．
解答 解：∵∠AOD=120°，
∴∠AOB=180°-∠AOD=180°-120°=60°，
∵四边形ABCD是矩形，
∴AO=BO=CO，
∴△AOB是等边三角形，
∴AO=AB=4cm，
∴AC=AO+CO=4+4=8cm．
故答案为：8cm．
点评 本题考查了矩形的性质，等边三角形的判定与性质，熟记各性质并判断出△AOB是等边三角形是解题的关键．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
12．下列各组数，可以作为直角三角形的三边长的是（ ）
| A． | 2，3，4 | B． | 3，4，5 | C． | 4，5，6 | D． | 5，6，7 |
如图，己知A（2$\sqrt{3}$，2），B（2$\sqrt{3}$，1）），将△AOB绕着点O逆时针旋转，使点A旋转到A′（-2，2$\sqrt{3}$）的位罝，则图中线段AB扫过的区域（即阴影部分）的面积为$\frac{3}{4}$π．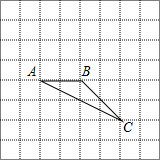
如图在8×8的正方形网格中，△ABC的顶点在边长为1的小正方形的顶点上．