题目内容
11.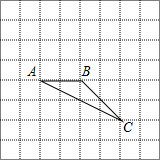 如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.
如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.(1)填空:∠ABC=135°,BC=2$\sqrt{2}$.
(2)若点A在网格所在的坐标平面里的坐标为(1,-2),请你在图中找出一点D,写出以A、B、C、D四个点为顶点的四边形是平行四边形,在图中标出满足条件的D点位置,并直接写出D点坐标.
分析 (1)直接利用网格得出:∠ABC的度数,再利用勾股定理得出BC的长;
(2)利用平行四边形的性质得出D点位置即可.
解答 解:(1)由图形可得:∠ABC=45°+90°=135°,BC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$;
故答案为:135°,2$\sqrt{2}$;
(2)∵点A在网格所在的坐标平面里的坐标为(1,-2),∴坐标系如图所示:
满足条件的D点共有3个,以A、B、C、D四个点为顶点的平行四边形分别是?ABCD1、?ABD2C 和?AD3BC.
则点D的坐标为:D1(3,-4)或D2(7,-4)或D3(-1,0).
点评 此题主要考查了平行四边形的判定、正方形的性质、勾股定理;注意不要漏解.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
1.我市某一周的最高气温统计如表,则这组数据的中位数是27℃.
| 最高气温(℃) | 25 | 26 | 27 | 28 |
| 天 数 | 1 | 2 | 1 | 3 |
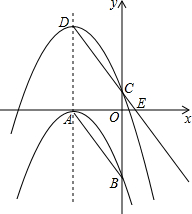 如图,抛物线C1:y=-$\frac{4}{9}$(x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E,
如图,抛物线C1:y=-$\frac{4}{9}$(x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E, 如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=4cm,则矩形的对角线长为8cm.
如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=4cm,则矩形的对角线长为8cm.
 如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM的长分别为2$\sqrt{3}$.
如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM的长分别为2$\sqrt{3}$.