题目内容
12.下列各组数,可以作为直角三角形的三边长的是( )| A. | 2,3,4 | B. | 3,4,5 | C. | 4,5,6 | D. | 5,6,7 |
分析 根据勾股定理的逆定理,验证四个选项中数据是否满足“较小两边平方的和等于最大边的平方”,由此即可得出结论.
解答 解:A、22+32=14,42=16,
∵14≠16,
∴2,3,4不能作为直角三角形的三边长;
B、32+42=25,52=25,
∵25=25,
∴3,4,5可以作为直角三角形的三边长;
C、42+52=41,62=36,
∵41≠36,
∴4,5,6不能作为直角三角形的三边长;
D、52+62=61,72=49,
∵61≠49,
∴5,6,7不能作为直角三角形的三边长.
故选B.
点评 本题考查了勾股定理的逆定理,解题的关键是根据勾股定理的逆定理验证四个选项.本题属于基础题,难度不大,解决该题型题目时,套入数据验证“较小两边平方的和是否等于最大边的平方”是关键.

练习册系列答案
相关题目
3. 如图,AB∥CD,CD∥EF,∠1=115°,则∠2的度数是( )
如图,AB∥CD,CD∥EF,∠1=115°,则∠2的度数是( )
 如图,AB∥CD,CD∥EF,∠1=115°,则∠2的度数是( )
如图,AB∥CD,CD∥EF,∠1=115°,则∠2的度数是( )| A. | 115° | B. | 85° | C. | 75° | D. | 65° |
7.下列运算正确的是( )
| A. | x6÷x3=x2 | B. | (-2x)3=-8x3 | C. | x6•x4=x24 | D. | (x3)3=x6 |
4.下列说法正确的是( )
| A. | -64的立方根是4 | B. | 9的平方根是±3 | ||
| C. | 4的算术平方根是16 | D. | 0.1的立方根是0.001 |
 如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解是-3.
如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解是-3.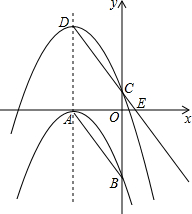 如图,抛物线C1:y=-$\frac{4}{9}$(x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E,
如图,抛物线C1:y=-$\frac{4}{9}$(x+3)2与x,y轴分别相交于点A,B,将抛物线C1沿对称轴向上平移,记平移后的抛物线为C2,抛物线C2的顶点是D,与y轴交于点C,射线DC与x轴相交于点E, 如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=4cm,则矩形的对角线长为8cm.
如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=4cm,则矩形的对角线长为8cm.