题目内容
1.已知实数a、b满足ab=1,a+b=3.(1)求代数式a2+b2的值;
(2)求a4-b4的值.
分析 (1)根据完全平分公式可得:a2+b2=(a+b)2-2ab,即可解答.
(2)利用完全平方公式及平方差公式,即可解答.
解答 解:(1)a2+b2=(a+b)2-2ab=32-2×1=9-2=7;
(2)∵(a-b)2=(a+b)2-4ab=32-4×1=5,
即a-b=$\sqrt{5}$,或a-b=-$\sqrt{5}$,
则a2-b2=(a-b)(a+b)=±3$\sqrt{5}$,
a4-b4=(a2+b2)(a2-b2)=7×$(±3\sqrt{5})=±21\sqrt{5}$.
点评 本题考查完全平分公式和平方差公式,解决本题的关键是熟记完全平分公式和平方差公式.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
12.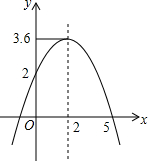 二次函数y=ax2+bx+c的图象如图所示.有下列结论:①a-b+c=0;②4a+b=0;③当y=2时,x等于0;④ax2+bx+c=-4有两个不相等的实数根.其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示.有下列结论:①a-b+c=0;②4a+b=0;③当y=2时,x等于0;④ax2+bx+c=-4有两个不相等的实数根.其中正确的个数是( )
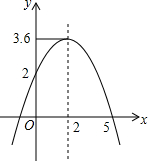 二次函数y=ax2+bx+c的图象如图所示.有下列结论:①a-b+c=0;②4a+b=0;③当y=2时,x等于0;④ax2+bx+c=-4有两个不相等的实数根.其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示.有下列结论:①a-b+c=0;②4a+b=0;③当y=2时,x等于0;④ax2+bx+c=-4有两个不相等的实数根.其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.化简$\frac{{a}^{2}+4a+4}{{a}^{2}-4}$÷($\frac{{a}^{2}}{a-2}$+$\frac{2a}{a-2}$)的结果是( )
| A. | $\frac{a}{a+2}$ | B. | $\frac{1}{a}$ | C. | $\frac{1}{a+2}$ | D. | $\frac{1}{a-2}$ |
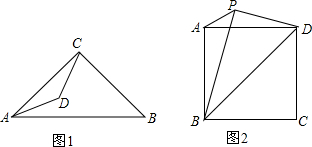
 △ABC中,点D在边AC上,AB=AC,AD=BD=BC,求出∠A的度数.
△ABC中,点D在边AC上,AB=AC,AD=BD=BC,求出∠A的度数.