题目内容
11.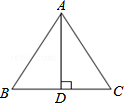 如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )
如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )| A. | BD=CD | B. | ∠DAB=∠DAC | ||
| C. | 当∠B=60°时,AB=2BD | D. | 高AD是△ABC的对称轴 |
分析 直接根据等腰三角形的性质可判断出A、B正确,再由直角三角形的性质可得出C正确,由对称轴的定义及等腰三角形的性质可对D进行判断.
解答 解:A、∵等腰△ABC中,AB=AC,AD⊥BC,
∴BD=CD,故此选项正确;
B、∵AB=AC,AD⊥BC,
∴∠DAB=∠DAC,故此选项正确;
C、∵∠B=60°,
∴∠BAD=90°-60°=30°,
∴AB=2BD,故此选项正确;
D、∵AD⊥BC,
∴直线AD是△ABC的对称轴,故D错误.
故选D.
点评 本题考查的是等腰三角形的性质,熟知等腰三角形三线合一的性质是解答此题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
1.以下说法正确的是( )
| A. | 调查某食品添加剂是否超标宜用普查 | |
| B. | 甲、乙两组的平均成绩相同,方差分别是S甲2=3.6,S乙2=3.0,则两组成绩一样稳定 | |
| C. | 同一年出生的367名学生中,至少有两人的生日是同一天是随机事件 | |
| D. | 调查10名运动员兴奋剂的使用情况适宜全面调查 |
3.下列是一元一次方程的是( )
| A. | x2-3=0 | B. | 3x+y=0 | C. | 5x+4 | D. | 3-2y=0 |
 三个有理数a、b、c在数轴上的位置如图所示,则a+b,a+c,b+c从大到小的顺序是a+b>a+c>b+c.(用“>”号连接)
三个有理数a、b、c在数轴上的位置如图所示,则a+b,a+c,b+c从大到小的顺序是a+b>a+c>b+c.(用“>”号连接)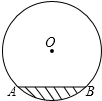 如图,水平放着的圆柱形水管的截面半径是12,其中水面的高为6,求水面AB的宽度是多少?
如图,水平放着的圆柱形水管的截面半径是12,其中水面的高为6,求水面AB的宽度是多少?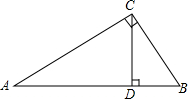 如图,Rt△ABC中,CD是斜边AB上的高.求证:
如图,Rt△ABC中,CD是斜边AB上的高.求证: