题目内容
9．一元二次方程（x-$\sqrt{5}$）（x+$\sqrt{5}$）+（2x-1）2=0化成一般形式正确的是（ ）| A． | 5x2-4x-4=0 | B． | x2-5=0 | C． | 5x2-2x+1=0 | D． | 5x2-4x+6=0 |
分析 直接利用完全平方公式以及平方差公式去括号，进而得出答案．
解答 解：（x-$\sqrt{5}$）（x+$\sqrt{5}$）+（2x-1）2=0
去括号得：x2-5+4x2-4x+1=0，
整理得：5x2-4x-4=0．
故选：A．
点评 此题主要考查了一元二次方程的一般形式，正确应用公式是解题关键．
练习册系列答案
备战中考寒假系列答案
相关题目
4．若点P（2k-1，2-k）在第二象限，则k的取值范围是（ ）
| A． | k＜$\frac{1}{2}$ | B． | k＜2 | C． | $\frac{1}{2}$＜k＜2 | D． | k＞2 |
14．若3x=4，9y=7，则3x+2y的值为（ ）
| A． | 28 | B． | 3 | C． | 11 | D． | 47 |
18．当x=3时，下列不等式成立的是（ ）
| A． | x+3＞5 | B． | x+3＞6 | C． | x+3＞7 | D． | x+3＜5 |
19．
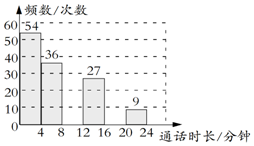手机在现如今的社会几乎是每人一部，在近期的一项研究结果显示，普通用户平均每天查看手机大约110次，其中大约22次是打电话．小乔想了解家人打电话的通话时长（即每次的通话时间）的分布情况，于是他收集了他家800个通话时长的数据，这些数据均不超过24分钟，他从中随机选取了若干个数据作为样本，统计结果如下表，并将结果绘制成如图所示的频数分布直方图．
（1）a的值为3；补全频数分布直方图；
（2）样本中通话时长在20＜x≤24之间的9个数据分别为21分08秒，22分25秒，22分14秒，21分23秒，23分48秒，21分02秒，23分16秒，23分42秒，21分17秒，求这9个通话时长的平均数；
（3）请估计小乔家这800个通话中通话时长超过12分钟的次数．
手机在现如今的社会几乎是每人一部，在近期的一项研究结果显示，普通用户平均每天查看手机大约110次，其中大约22次是打电话．小乔想了解家人打电话的通话时长（即每次的通话时间）的分布情况，于是他收集了他家800个通话时长的数据，这些数据均不超过24分钟，他从中随机选取了若干个数据作为样本，统计结果如下表，并将结果绘制成如图所示的频数分布直方图．| 通话时长x/分钟 | 次数 |
| 0＜x≤4 | 54 |
| 4＜x≤8 | 36 |
| 8＜x≤12 | 4a |
| 12＜x≤16 | 27 |
| 16＜x≤20 | 4a |
| 20＜x≤24 | 3a |
（2）样本中通话时长在20＜x≤24之间的9个数据分别为21分08秒，22分25秒，22分14秒，21分23秒，23分48秒，21分02秒，23分16秒，23分42秒，21分17秒，求这9个通话时长的平均数；
（3）请估计小乔家这800个通话中通话时长超过12分钟的次数．