题目内容
6.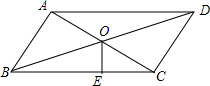 如图,在平行四边形ABCD中,连接AC、BD,AD=5,BD=2$\sqrt{10}$,tan∠DBC=$\frac{1}{3}$,则平行四边形ABCD的面积是10.
如图,在平行四边形ABCD中,连接AC、BD,AD=5,BD=2$\sqrt{10}$,tan∠DBC=$\frac{1}{3}$,则平行四边形ABCD的面积是10.
分析 首先过点D作DF⊥BC于点F,由BD=2$\sqrt{10}$,tan∠DBC=$\frac{1}{3}$,可求得DF的长,继而求得平行四边形ABCD的面积.
解答  解:过点D作DF⊥BC于点F,
解:过点D作DF⊥BC于点F,
∵tan∠DBC=$\frac{1}{3}$,
∴sin∠DBC=$\frac{\sqrt{10}}{10}$,
∴DF=BD•sin∠DBC=2$\sqrt{10}$×$\frac{\sqrt{10}}{10}$=2,
∵在平行四边形ABCD中,AD=5,
∴BC=AD=5,
∴平行四边形ABCD的面积是:BC•DF=5×2=10.
故答案为:10.
点评 此题考查了平行四边形的性质以及三角函数的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
11.若x1,x2是x2-x-3=0的两个实数根,则-x1-x2=( )
| A. | ±1 | B. | -3 | C. | -1 | D. | 3 |
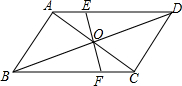 如图,?ABCD的对角线AC,BD相交于点O,EF经过点O且与AD,BC分别交于点E,F,已知AB=4,BC=5,OE=1.
如图,?ABCD的对角线AC,BD相交于点O,EF经过点O且与AD,BC分别交于点E,F,已知AB=4,BC=5,OE=1.