题目内容
17.菱形ABCD中,边长AB=2,∠A=45°,则菱形ABCD的面积是( )| A. | 4 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | $\sqrt{2}$ |
分析 如图,作BH⊥AD于H.在Rt△ABH中,先求出BH,根据菱形ABCD的面积=AD•BH即可解决问题.
解答 解:如图, 作BH⊥AD于H.
作BH⊥AD于H.
在Rt△ABH中,∵∠AHB=90°,AB=2,∠A=45°,
∴BH=AB•sin45°=$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$,
∵四边形ABCD是菱形,
∴AB=AD=2,
∴菱形ABCD的面积=AD•BH=2$\sqrt{2}$.
故选B.
点评 本题考查菱形的性质,解直角三角形等知识,解题的关键是记住菱形的两种面积公式,属于基础题,中考常考题型.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
5.下列方程是一元一次方程的是( )
| A. | x=0 | B. | y2-2y-1=0 | C. | $\frac{1}{3}$x-$\frac{3}{x}$=2 | D. | 2x+3y=1 |
12.二元一次方程组$\left\{\begin{array}{l}{x+3y=2}\\{2x-3y=1}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=\frac{1}{3}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-\frac{1}{3}}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-\frac{1}{3}}\end{array}\right.$ |
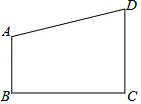 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的四边形,AB∥CD,CD⊥BC于C,且AB、BC、CD边长分别为2,4,3,则原直角三角形纸片的斜边长是4$\sqrt{5}$或10.
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的四边形,AB∥CD,CD⊥BC于C,且AB、BC、CD边长分别为2,4,3,则原直角三角形纸片的斜边长是4$\sqrt{5}$或10.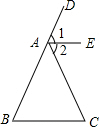 已知,如图∠B=∠C,∠DAC=∠B+∠C,AE平分∠DAC,AE∥BC吗?为什么?
已知,如图∠B=∠C,∠DAC=∠B+∠C,AE平分∠DAC,AE∥BC吗?为什么?