题目内容
3.请用科学的方法证明圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.分析 (1)利用三角形外角的性质求解即可求得答案;
(2)应该是连接OA,∠COB=∠A+∠B+∠C=2∠A.
(3)应该是连接AO并延长交圆于点D,∠COD=2∠OAC,∠BOD=2∠OAB,∠BOC=∠COD-∠BOD=2(∠OAC-∠OAB)=2∠BAC
解答 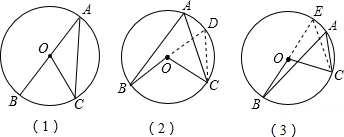 证明:①如图(1),当点O在∠BAC的一边上时,
证明:①如图(1),当点O在∠BAC的一边上时,
∵OA=OC,
∴∠A=∠C,
∵∠BOC=∠A+∠C,
∴∠BAC=$\frac{1}{2}$∠BOC;
②如图(2)当圆心O在∠BAC的内部时,延长BO交⊙O于点D,连接CD,则
∠D=∠A(同弧或等弧所对的圆周角都相等),
∵OC=OD,
∴∠D=∠OCD,
∵∠BOC=∠D+∠OCD(三角形的一个外角等于与它不相等的两个内角的和),
∴∠BOC=2∠A,
即∠BAC=$\frac{1}{2}$∠BOC.
③如图(3),当圆心O在∠BAC的外部时,延长BO交⊙O于点E,连接CE,则
∠E=∠A(同弧或等弧所对的圆周角都相等),
∵OC=OE,
∴∠E=∠OCE,
∵∠BOC=∠E+∠OCE(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠BOC=2∠A,
即∠BAC=$\frac{1}{2}$∠BOC.
点评 此题考查了圆周角定理以及等腰三角形的判定与性质.注意掌握分类讨论思想的应用是解此题的关键.

练习册系列答案
相关题目
11.绵阳市作为全国居民健康卡建设试点城市,尤其是在卫生信息化建设方面,绵阳市累计投入资金2亿余元,综合数据平台和卫生信息化专(兼)职队伍初步建立,其中2亿用科学记数法表示为( )
| A. | 20×108 | B. | 2×108 | C. | 0.2×108 | D. | 2×107 |
15.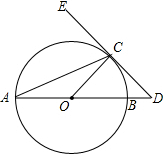 如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )
如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )
 如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )
如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )| A. | 30° | B. | 45° | C. | 60° | D. | 67.5° |
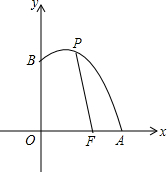 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论: