题目内容
16.已知x2+3x-1=0,求x-$\frac{1}{x}$和$x+\frac{1}{x}$的值.分析 已知等式两边除以x求出x-$\frac{1}{x}$的值,再利用完全平方公式求出x+$\frac{1}{x}$的值即可.
解答 解:已知x2+3x-1=0,变形得:x-$\frac{1}{x}$=-3,
两边平方得:x2+$\frac{1}{{x}^{2}}$-2=9,即x2+$\frac{1}{{x}^{2}}$=11,
则(x+$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$+2=13,即x+$\frac{1}{x}$=±$\sqrt{13}$.
点评 此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
4.一艘轮船从港口A出发向东北方向航行7km,另一艘轮船也从港口A出发向东南方向航行了12km,此时两艘轮船相距( )
| A. | 5km | B. | $\sqrt{193}$km | C. | 19km | D. | 193km |
1.抛物线y=$\frac{1}{2}$(x+2)(x-6)的对称轴是( )
| A. | 直线x=-2 | B. | 直线x=6 | C. | 直线x=2 | D. | 直线x=4 |
5.将a+b-4(a+b)合并同类项,得( )
| A. | 3a+3b | B. | -3a-3b | C. | 4b-3a | D. | 3a-3b |
13. 如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
 如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )
如图是某校食堂甲、乙、丙、丁四种午餐受欢迎程度的扇形统计图,则最受欢迎的午餐是( )| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
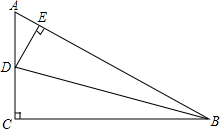 如图,D是△ACB的边AC上一点,AC⊥BC,DE⊥AB,垂足分别为点C,E,∠A=60°,DC=DE,求∠DBC的度数.
如图,D是△ACB的边AC上一点,AC⊥BC,DE⊥AB,垂足分别为点C,E,∠A=60°,DC=DE,求∠DBC的度数.