题目内容
9.已知在Rt△ABC中,∠ACB=90°,AB=3.(1)分别以AB、AC、BC为直角边向形外作等腰直角三角形,求阴影部分的面积之和为$\frac{9}{2}$;
(2)分别以AB、AC、BC为长向形外作长方形,使宽是长的$\frac{3}{4}$,求阴影部分的面积之和为$\frac{27}{2}$.
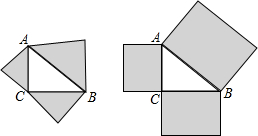
分析 (1)由勾股定理得出AC2+BC2=AB2=9,由等腰三角形的性质即可求出阴影部分的面积之和;
(2)由勾股定理得出AC2+BC2=AB2=9,由长方形的性质和宽与长的关系即可求出阴影部分的面积之和.
解答 解:(1)∵∠ACB=90°,AB=3,
∴AC2+BC2=AB2=9,
∴阴影部分的面积之和=$\frac{1}{4}$AC2+$\frac{1}{4}$BC2+$\frac{1}{4}$AB2=$\frac{1}{4}$×9+$\frac{1}{4}$×9=$\frac{9}{2}$;
故答案为:$\frac{9}{2}$;
(2)∵∠ACB=90°,AB=3,
∴AC2+BC2=AB2=9,
∴阴影部分的面积之和=$\frac{3}{4}$AC2+$\frac{3}{4}$BC2+$\frac{3}{4}$AB2=$\frac{3}{4}$(9+9)=$\frac{27}{2}$;
故答案为$\frac{27}{2}$.
点评 本题考查了等腰直角三角形的性质、勾股定理、长方形的性质、阴影部分面积的计算;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
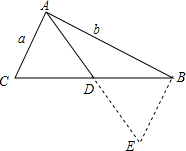 如图所示,在三角形中已知两边之长分别为a,b(a<b),那么第三边上的中线的长度x的取值范围是$\frac{b-a}{2}$<x<$\frac{b+a}{2}$.
如图所示,在三角形中已知两边之长分别为a,b(a<b),那么第三边上的中线的长度x的取值范围是$\frac{b-a}{2}$<x<$\frac{b+a}{2}$.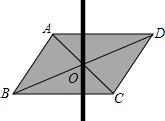 用硬纸板剪一个平行四边形,做出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处.若木条与AD交于点E、与BC交于点F,拨动细木条
用硬纸板剪一个平行四边形,做出它的对角线的交点O,用大头针把一根平放在平行四边形上的直细木条固定在点O处.若木条与AD交于点E、与BC交于点F,拨动细木条