题目内容
4．已知x=$\sqrt{3}$+1，那么代数式$\frac{{{x^4}+4}}{{{x^2}+2x+2}}$的值为4．分析 先化简，再把x=$\sqrt{3}$+1代入求值即可．
解答 解：$\frac{{{x^4}+4}}{{{x^2}+2x+2}}$=$\frac{{x}^{4}+4}{（x+1）^{2}+1}$=$\frac{（\sqrt{3}+1）^{4}+4}{（\sqrt{3}+1+1）^{2}+1}$=$\frac{32+16\sqrt{3}}{8+4\sqrt{3}}$=4．
故答案为：4．
点评 本题主要考查了分式的化简求值，细心计算是解题的关键．
练习册系列答案
53随堂测系列答案
相关题目
15．
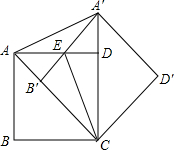如图，把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′（此时，点B′落在对角线AC上，点A′落在CD的延长线上），A′B′交AD于点E，连接AA′、CE．求证：AA′=CE．
如图，把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′（此时，点B′落在对角线AC上，点A′落在CD的延长线上），A′B′交AD于点E，连接AA′、CE．求证：AA′=CE． 
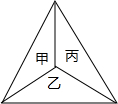如图，一只蚊子在甲、乙、丙三个房间之间飞来飞去，蚊子从一个房间随机飞到另一个房间，共飞三次．
如图，已知△ABC中，∠A=58°，如果：（1）O为外心；（2）O为内心；（3）O为垂心．分别求以上三种条件下的∠BOC的度数．
13．下列各数中无理数是（ ）
| A． | 0.1010010001 | B． | $\sqrt{9}$ | C． | $\root{3}{-64}$ | D． | $\frac{π}{2}$ |
