题目内容
19.某同学在电脑中打出如下排列的若干个圆(圆中●表实心圆,○表空心圆):●○●●○●●●○●●●●○●●●●●○●●●●●●○,若将上面一组圆依此规律连续复制一系列圆,那么前2005个圆中有61个空心圆.分析 首先根据图示,可得每个空心圆的前面相邻的实心圆的个数分别是1、2、3、4、5、6、…,然后根据●○、●●○、●●●○、●●●●○、●●●●●○、●●●●●●○的个数分别是2、3、4、5、6、7、…,求出前n组圆的总数是多少个,进而判断出前2005个圆中有多少个空心圆即可.
解答 解:∵●○、●●○、●●●○、●●●●○、●●●●●○、●●●●●●○的个数分别是2、3、4、5、6、7、…,
∴前n组圆的总数是:(n+1+2)n÷2=$\frac{1}{2}n(n+3)$,
∵$\frac{1}{2}×61×(61+3)=1952$,$\frac{1}{2}×62×(62+3)=2015$,1952<2005<2015,
∴前2005个圆中有61个空心圆.
故答案为:61.
点评 此题主要考查了图形的变化类问题,要熟练掌握,解答此类问题的关键是首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.

练习册系列答案
相关题目
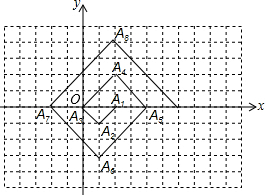 如图,在单位为1的正方形网格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2015的坐标为(-1006,0).
如图,在单位为1的正方形网格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2015的坐标为(-1006,0).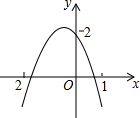 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论
如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论