Question

18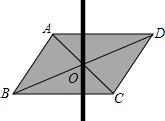．用硬纸板剪一个平行四边形，做出它的对角线的交点O，用大头针把一根平放在平行四边形上的直细木条固定在点O处．若木条与AD交于点E、与BC交于点F，拨动细木条
（1）OE=OF吗？为什么？
（2）什么情况下ABFE为平行四边形？为什么？什么情况下ABFE为等腰梯形？为什么？
（3）什么情况下AFCE为菱形？为什么？

Answer 1

分析 （1）由四边形ABCD是平行四边形，可得AD∥BC，OA=OC，继而证得△AOE≌△COF（ASA），则可证得结论；
（2）根据平行四边形的判定和等腰梯形的判定解答即可；
（3）根据菱形的判定解答即可．

解答 解：（1）OE=OF．
理由：∵四边形ABCD是平行四边形，
∴AD∥BC，OA=OC，
∴∠OAE=∠OCF，
在△AOE和△COF中，
$\left\{\begin{array}{l}{∠AOE=∠COF}\\{OA=OC}\\{∠OAE=∠OCF}\end{array}\right.$，
∴△AOE≌△COF（ASA），
∴OE=OF；
（2）当EF∥AB时，四边形ABFE为平行四边形；
∵AE∥BF，EF∥AB，
∴四边形ABFE为平行四边形；
当EF=AB时，四边形ABFE为等腰梯形；
∵AE∥BF，EF=AB，
∴四边形ABFE为等腰梯形；
（3）当AB=BF时，四边形ABFE为菱形；
∵AE∥BF，AE=BF，AB=BF，
∴四边形ABFE为菱形．

点评 此题考查了平行四边形的性质以及全等三角形的判定与性质．注意证得△AOE≌△COF是解此题的关键．