题目内容
14.已知三个自然数a,b,c中至少a为质数,且满足$\left\{\begin{array}{l}{(4a+2b-4c)^{2}=443(2a-442b+884c)}\\{\sqrt{4a+2b-4c+886}-\sqrt{442b-2a+2c-443}=\sqrt{443}}\end{array}\right.$,试求abc的值.分析 首先将已知条件变形得出2a+b-2c是443的倍数,进而令2a+b-2c=443k,再得出a与k的函数关系式,进而利用a为质数得出a的值,进而结合所求得出b,c的值.
解答 解:由已知可得:2(2a+b-2c)2=443(a-221b+442c),
由于443是质数,故2a+b-2c是443的倍数,
令2a+b-2c=443k①,
∴a-221b+442c=886k2②,
①-②得:a+222b-444c=443k-886k2,
∴a=443k-886k2+222(2c-b),
①+②得:886c-443b=1772k2-443k,
∴2c-b=4k2-k,
∴a=443k-886k2+222(4k2-k)=2k2+221k=k(2k+221)
由于a为质数,2k+221≠1,
故k=1,a=2k+221=223,
将①②代入原方程得:
代入(2)得:$\sqrt{886k+886}$-$\sqrt{886c-443-1772{k}^{2}}$=$\sqrt{443}$,
∴$\sqrt{2k+2}$-$\sqrt{2c-1-4{k}^{2}}$=1,
∴2-$\sqrt{2c-2}$=1,
解得:c=3,
∴6-b=3,从而b=3,
∴abc=2007.
点评 此题主要考查了质数的应用,根据题意得出2a+b-2c是443的倍数,进而利用换元法得出a的值是解题关键.

练习册系列答案
相关题目
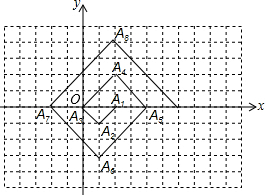 如图,在单位为1的正方形网格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2015的坐标为(-1006,0).
如图,在单位为1的正方形网格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2015的坐标为(-1006,0). 已知:如图,∠AEB=∠ADB=90°,C为AB的中点,连接CD、CE、DE,求证:△CDE为等腰三角形.
已知:如图,∠AEB=∠ADB=90°,C为AB的中点,连接CD、CE、DE,求证:△CDE为等腰三角形.