题目内容
20．
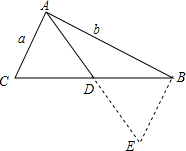如图所示，在三角形中已知两边之长分别为a，b（a＜b），那么第三边上的中线的长度x的取值范围是$\frac{b-a}{2}$＜x＜$\frac{b+a}{2}$．
分析 首先延长AD到E，使DE=AD，连接BE，证明△ACD≌△EBD可得AC=BE=a，再根据三角形的三边关系可得AB-EB＜AE＜AB+BE，进而可得b-a＜2AD＜b+a，从而可得答案．
解答 解：延长AD到E，使DE=AD，连接BE；
∵AD为中线，
∴CD=BD，
在△ACD和△EBD中$\left\{\begin{array}{l}{AD=DE}\\{∠ADC=∠BDE}\\{CD=BD}\end{array}\right.$，
∴△ACD≌△EBD（SAS），
∴EB=AC=a，
∵在△AEB中，AB-EB＜AE＜AB+BE，
∴b-a＜2AD＜b+a，
∴$\frac{b-a}{2}$＜x＜$\frac{b+a}{2}$，
故答案为：$\frac{b-a}{2}$＜x＜$\frac{b+a}{2}$．
点评 此题主要考查了三角形的三边关系，关键是正确作出辅助线，构造全等三角形．
练习册系列答案
相关题目
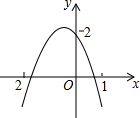如图所示，二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），且与x轴交点的横坐标分别为x1，x2，其中-2＜x1＜-1，0＜x2＜1，下列结论
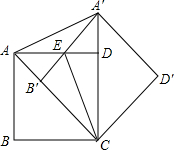如图，把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′（此时，点B′落在对角线AC上，点A′落在CD的延长线上），A′B′交AD于点E，连接AA′、CE．求证：AA′=CE．
已知：如图，∠AEB=∠ADB=90°，C为AB的中点，连接CD、CE、DE，求证：△CDE为等腰三角形．
