题目内容
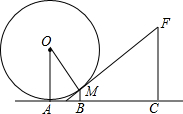 如图,一个小朋友玩“滚铁环”游戏,铁环是圆形的,铁环向前滚动时,铁环与铁钩相切,这个游戏抽象为数学问题,如图,已知铁环的半径为25cm,铁环中心为O,铁环钩与铁环相切点为M,铁环也地面接触点为A,且sin∠MOA=
如图,一个小朋友玩“滚铁环”游戏,铁环是圆形的,铁环向前滚动时,铁环与铁钩相切,这个游戏抽象为数学问题,如图,已知铁环的半径为25cm,铁环中心为O,铁环钩与铁环相切点为M,铁环也地面接触点为A,且sin∠MOA=| 3 |
| 5 |
(1)求点M离地面AC的高度BM.
(2)设人站立点C与A点的水平距离AC=55cm,求铁环钩MF的长度.
考点:切线的性质,解直角三角形的应用
专题:
分析:(1)过M作与AC平行的直线,与OA、FC分别相交于H、N.那么求BM的长就转化为求HA的长,而要求出HA,必须先求出OH,在直角三角形OHM中,sinα的值,且铁环的半径为5个单位即OM=5,可求得HM的值,从而求得HA的值;
(2)因为∠MOH+∠OMH=∠OMH+∠FMN=90°,∠FMN=∠MOH,又因为sin∠MOA=
,所以可得出FN和FM之间的数量关系,即FN=
FM,再根据MN=11-3=8,利用勾股定理即可求出FM=10个单位.
(2)因为∠MOH+∠OMH=∠OMH+∠FMN=90°,∠FMN=∠MOH,又因为sin∠MOA=
| 3 |
| 5 |
| 3 |
| 5 |
解答: 解:过M作与AC平行的直线,与OA、FC分别相交于H、N.
解:过M作与AC平行的直线,与OA、FC分别相交于H、N.
(1)在Rt△OHM中,∠OHM=90°,OM=25,
HM=OM×sinα=15,
所以OH=20,
MB=HA=25-20=5,
所以铁环钩离地面的高度为5cm;
(2)∵铁环钩与铁环相切,
∴∠MOH+∠OMH=∠OMH+∠FMN=90°,∠FMN=∠MOH,
∴
=sin∠MOA=
,
∴FN=
FM,
在Rt△FMN中,∠FNM=90°,MN=BC=AC-AB=55-15=40.
∵FM2=FN2+MN2
即FM2=(
FM)2+402,
解得:FM=50,
∴铁环钩的长度FM为50cm.
 解:过M作与AC平行的直线,与OA、FC分别相交于H、N.
解:过M作与AC平行的直线,与OA、FC分别相交于H、N.(1)在Rt△OHM中,∠OHM=90°,OM=25,
HM=OM×sinα=15,
所以OH=20,
MB=HA=25-20=5,
所以铁环钩离地面的高度为5cm;
(2)∵铁环钩与铁环相切,
∴∠MOH+∠OMH=∠OMH+∠FMN=90°,∠FMN=∠MOH,
∴
| FN |
| FM |
| 3 |
| 5 |
∴FN=
| 3 |
| 5 |
在Rt△FMN中,∠FNM=90°,MN=BC=AC-AB=55-15=40.
∵FM2=FN2+MN2
即FM2=(
| 3 |
| 5 |
解得:FM=50,
∴铁环钩的长度FM为50cm.
点评:考查了解直角三角形的应用,解此题的关键是把实际问题转化为数学问题,只要把实际问题抽象到解直角三角形中即可解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,顶点C在y轴上,OA、OB的长是关于x的方程x2-25x+144=0的两个根(OA>OB).
如图所示,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,顶点C在y轴上,OA、OB的长是关于x的方程x2-25x+144=0的两个根(OA>OB).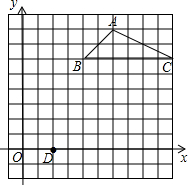 作图题:我们把顶点在正方形网格交点上的图形叫做格点图形,如图,△ABC就是一个格点三角形,图中的正方形网格边长为1个单位长度.
作图题:我们把顶点在正方形网格交点上的图形叫做格点图形,如图,△ABC就是一个格点三角形,图中的正方形网格边长为1个单位长度.
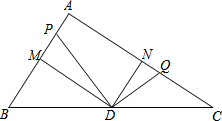 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点M、N分别为AB,AC边的中点,点D为BC边的中点,动点P从点A出发,沿射线AB方向移动,作∠PDQ=90°,点Q在AC上,设AP=x,CQ=y.
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点M、N分别为AB,AC边的中点,点D为BC边的中点,动点P从点A出发,沿射线AB方向移动,作∠PDQ=90°,点Q在AC上,设AP=x,CQ=y. 如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高BE=8米,求小船C到岸边的距离CA的长?(参考数据:
如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高BE=8米,求小船C到岸边的距离CA的长?(参考数据: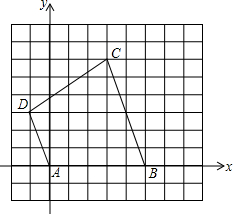 如图,在10×10的正方形网格纸中,A(0,0),B(5,0),C(3,6),D(-1,3),依次连接A、B、C、D四点得到四边形ABCD.
如图,在10×10的正方形网格纸中,A(0,0),B(5,0),C(3,6),D(-1,3),依次连接A、B、C、D四点得到四边形ABCD.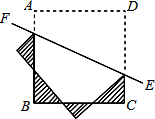 如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为
如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为