题目内容
20. Rt△ABC中,∠B=90°,AD平分∠BAC,BD=2cm,AC=5cm,则S△ADC=5cm2.
Rt△ABC中,∠B=90°,AD平分∠BAC,BD=2cm,AC=5cm,则S△ADC=5cm2.
分析 过D作DE⊥AC于E,根据角平分线性质求出DE=BD=2cm,根据三角形面积公式求出即可.
解答 解:
过D作DE⊥AC于E,
∵∠B=90°,AD平分∠BAC,BD=2cm,
∴DE=BD=2cm,
∵AC=5cm,
∴S△ADC=$\frac{1}{2}$×AC×DE=5cm2,
故答案为:5.
点评 本题考查了角平分线性质的应用,能根据角平分线性质得出DE=BD=2cm是解此题的关键,注意:角平分线上的点到这个角的两边的距离相等.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
11.函数y=$\frac{2015}{x}$中,自变量x的取值范围是( )
| A. | x>0 | B. | x<0 | C. | x≠0的一切实数 | D. | x取任意实数 |
15.将一些半径相同的小圆按如图所示的规律摆放,请仔细观察,第n个图形的小圆个数是( )(用含有n的代数式表示)
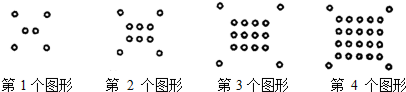

| A. | 4n+(n+1) | B. | n2+4n | C. | 4+n(n+1) | D. | 4+(n+1)2 |
5.已知两点A(5,6),B(7,2),先将线段AB向左平移一个单位,再以原点O为位似中心,将其缩小为原来的$\frac{1}{2}$得到线段CD,则点A的对应点C的坐标为( )
| A. | (2,3) | B. | (-2,-3) | C. | (2,3)或(-2,-3) | D. | (3,3)或(-3,-3) |
12. 如图,在△ABC中,∠C=90°,AC=2,BC=1,则cosA的值是( )
如图,在△ABC中,∠C=90°,AC=2,BC=1,则cosA的值是( )
 如图,在△ABC中,∠C=90°,AC=2,BC=1,则cosA的值是( )
如图,在△ABC中,∠C=90°,AC=2,BC=1,则cosA的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
10.已知反比例函数y=$\frac{k}{x}$(k<0)图象上有三点A(-3,a)、B(-1,b)、C(2,c),则a、b、c的大小关系是( )
| A. | c<a<b | B. | a<c<b | C. | b<c<a | D. | c<b<a |
 如图,线段AC=6,线段BC=16,点M是AC的中点,在线段CB上取一点N,使得CN=$\frac{1}{3}$NB,求MN的长.
如图,线段AC=6,线段BC=16,点M是AC的中点,在线段CB上取一点N,使得CN=$\frac{1}{3}$NB,求MN的长.