题目内容
3.已知直角三角形一边长为8,另一边长是方程x2-8x-20=0的根,求第三边的长.分析 先解方程求得另一条边是10,再分两种情况讨论求得即可.
解答 解:x2-8x-20=0,
(x-10)(x+2)=0,
所以x1=10,x2=-2,
所以另一边长是10,
①若10为斜边,则用勾股定理得第三条边长是:$\sqrt{1{0}^{2}-{8}^{2}}$=6;
②若10是直角边,则此直角三角形的第三条边长是:$\sqrt{1{0}^{2}+{8}^{2}}$=2$\sqrt{41}$.
点评 本题考查了勾股定理、解方程.解题的关键是要注意分情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




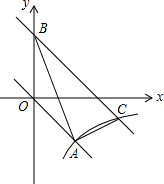 如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2).
如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象都经过点A(2,-2).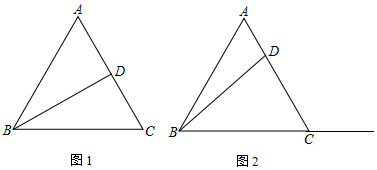
 如图,CE是△ABC的外角∠ACD的平分线,交BA的延长线于点E,若∠E=20°,∠B=30°,则∠BAC=70°.
如图,CE是△ABC的外角∠ACD的平分线,交BA的延长线于点E,若∠E=20°,∠B=30°,则∠BAC=70°.