题目内容
1.若关于x的不等式组$\left\{\begin{array}{l}{\frac{2}{3}-\frac{2x}{3}<1}\\{3x+a<5}\end{array}\right.$有且仅有四个整数解,则a的取值范围是-10≤a<-7.分析 首先解不等式组确定不等式组的解集,然后根据不等式组有四个整数解即可得到关于a的不等式组,求得a的值.
解答 解:$\left\{\begin{array}{l}{\frac{2}{3}-\frac{2}{3}x<1…①}\\{3x+a<5…②}\end{array}\right.$,
解①得:x>$\frac{1}{2}$,
解②得:x<$\frac{5-a}{3}$,
则不等式组的解集是:$\frac{1}{2}$<x<$\frac{5-a}{3}$.
不等式组有四个整数解,则是1,2,3,4.
则4<$\frac{5-a}{3}$≤5.
解得:-10≤a<-7.
故答案是:-10≤a<-7.
点评 本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
13.不等式组$\left\{\begin{array}{l}{4x<6+x}\\{x+3>2}\end{array}\right.$的解集是( )
| A. | -1<x<2 | B. | x>-1 | C. | x<2 | D. | -2<x<1 |
 如图,点E是?ABCD的边AD的中点,连接CE交BD于点F,如果S△DEF=a,那么S△BCF=4a.
如图,点E是?ABCD的边AD的中点,连接CE交BD于点F,如果S△DEF=a,那么S△BCF=4a.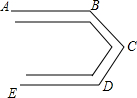 要修建一条如图所示的公路,AB∥DE,∠D=120°,为保证汽车的行驶安全,在C处拐弯的角度∠BCD不能低于100°,求在B处拐弯的角度最大是多少?
要修建一条如图所示的公路,AB∥DE,∠D=120°,为保证汽车的行驶安全,在C处拐弯的角度∠BCD不能低于100°,求在B处拐弯的角度最大是多少?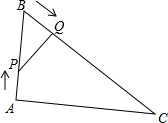 如图所示,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以1cm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q同时出发,经过多长时间后,△PBQ与△ABC相似?试说明理由.
如图所示,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以1cm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q同时出发,经过多长时间后,△PBQ与△ABC相似?试说明理由.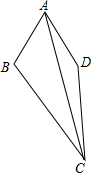 如图,四边形ABCD中,∠BAD=60°,∠BCD=30°,AB=AD,BC=8cm,CD=5cm,则AC的长为$\sqrt{89}$cm.
如图,四边形ABCD中,∠BAD=60°,∠BCD=30°,AB=AD,BC=8cm,CD=5cm,则AC的长为$\sqrt{89}$cm.