题目内容
9.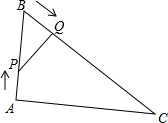 如图所示,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以1cm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q同时出发,经过多长时间后,△PBQ与△ABC相似?试说明理由.
如图所示,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以1cm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q同时出发,经过多长时间后,△PBQ与△ABC相似?试说明理由.
分析 首先设经x秒钟△PBQ与△ABC相似,由题意可得AP=xcm,BQ=2xcm,BP=AB-AP=(8-x)cm,又由∠B是公共角,分别从$\frac{BP}{BA}$=$\frac{BQ}{BC}$或$\frac{BP}{AC}$=$\frac{BQ}{BA}$分析,即可求得答案.
解答 解:设经x秒钟△PBQ与△ABC相似,
则AP=xcm,BQ=2xcm,
∵AB=8cm,BC=16cm,
∴BP=AB-AP=(8-x)cm,
∵∠B是公共角,
∵①当$\frac{BP}{BA}$=$\frac{BQ}{BC}$,即$\frac{8-x}{8}$=$\frac{2x}{16}$时,△PBQ∽△ABC,
解得:x=4;
②当$\frac{BP}{BC}$=$\frac{BQ}{BA}$,即$\frac{8-x}{16}$=$\frac{2x}{8}$时,△QBP∽△ABC,
解得:x=1.6,
∴经4或1.6秒钟△PBQ与△ABC相似.
点评 此题考查了相似三角形的判定.此题难度适中,属于动点型题目,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
相关题目
19.下列一元二次方程中,有两个相等实数根的是( )
| A. | x2-8=0 | B. | 2x2-4x+3=0 | C. | 9x2+6x+1=0 | D. | 5x+2=3x2 |
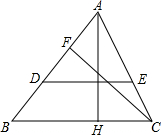 如图,在△ABC中,AH⊥BC于H,CF⊥AB于F,D是AB上一点,AD=AH,DE∥BC,求证:DE=CF.
如图,在△ABC中,AH⊥BC于H,CF⊥AB于F,D是AB上一点,AD=AH,DE∥BC,求证:DE=CF.