题目内容
4.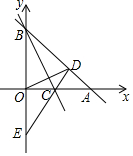 如图,在平面直角坐标系中,直线y=-x+2交x轴于点A,交y轴于点B,C是OA的中点,D为线段AB上一点,且∠ACD=∠BCO.
如图,在平面直角坐标系中,直线y=-x+2交x轴于点A,交y轴于点B,C是OA的中点,D为线段AB上一点,且∠ACD=∠BCO.(1)求BC的长;
(2)作直线CD交y轴于点E.
①求直线CD的解析式及点D的坐标;
②连结OD,求证:OD+CD=BC.
(3)P为x轴上一点,且到直线CD的距离等于BC长,求点P的坐标.
分析 (1)首先求出A、B两点坐标,根据勾股定理即可解决问题.
(2)①首先证明△BCE是等腰三角形,求出直线CD的解析式,列方程组即可求出点D坐标.
②求出OD、CD的长即可解决问题.
(3)如图,作P1M⊥CD于M,设P1(m,0).由△P1MC∽△BOC,得$\frac{{P}_{1}M}{OB}$=$\frac{{P}_{1}C}{BC}$,列出方程求出m,可得P1坐标,再根据对称性求出点P2坐标即可.
解答 解:(1)∵直线y=-x+2交x轴于点A,交y轴于点B,
∴A(2,0),B(0,2),
∵C是OA中点,OA=BO=2,
∴OC=AC=1,
在Rt△BCO中,BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
(2)①∵∠DCA=∠BCO,∠DCA=∠ECO,
∴∠OCB=∠OCE,
∵∠OCB+∠OBC=90°,∠OCE+∠OEC=90°,
∴∠OBC=∠OEC,
∴BC=EC,OB=OE=2,
∴E(0,-2),∵C(1,0),
∴直线CD的解析式为y=2x-2,
由$\left\{\begin{array}{l}{y=2x-2}\\{y=-x+2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=\frac{2}{3}}\end{array}\right.$,
∴点D坐标($\frac{4}{3}$,$\frac{2}{3}$).
②∵D($\frac{4}{3}$,$\frac{2}{3}$),C(1,0),
∴OD=$\sqrt{(\frac{4}{3})^{2}+(\frac{2}{3})^{2}}$=$\frac{2\sqrt{5}}{3}$.CD=$\sqrt{(\frac{4}{3}-1)^{2}+(\frac{2}{3})^{2}}$=$\frac{\sqrt{5}}{3}$,
∴OD+CD=$\frac{2\sqrt{5}}{3}$+$\frac{\sqrt{5}}{3}$=$\sqrt{5}$,
∵BC=$\sqrt{5}$,
∴CD+OD=BC.
(3)如图,作P1M⊥CD于M,设P1(M,0).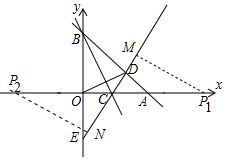
∵∠BOC=∠CMP1=90°,∠MCP1=∠BCO,
∴△P1MC∽△BOC,
∴$\frac{{P}_{1}M}{OB}$=$\frac{{P}_{1}C}{BC}$,
∴$\frac{\sqrt{5}}{2}$=$\frac{m-1}{\sqrt{5}}$,
∴m=$\frac{7}{2}$,
∴P1($\frac{7}{2}$,0),
根据对称性,P2与P1关于点C对称时,点P2到直线CD的距离为$\sqrt{5}$,
∴P2(-$\frac{3}{2}$,0),
综上所述,满足条件的点P坐标为($\frac{7}{2}$,0)或(-$\frac{3}{2}$,0).
点评 本题考查一次函数综合题、待定系数法、两点间距离公式、相似三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识,学会用方程的思想思考问题,属于中考常考题型.

①经过一点有且只有一条直线与已知直线平行;
②垂直于同一条直线的两条直线互相平行;
③直线外一点到这条直线的垂线段,叫做这个点到直线的距离;
④同一平面内不相交的两条直线叫做平行线.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 正三角形 | B. | 正四边形 | C. | 正五边形 | D. | 正六边形 |
| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
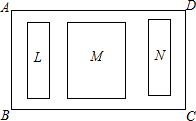 要对一块长60m.宽40m的矩形荒地ABCD(BC>AB)进行绿化和硬化,设计方案如图所示.矩形L、M、N为三块绿地.其余为硬化路面,L、M、N三块绿地周围的硬化路面宽都相等.并使三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$.
要对一块长60m.宽40m的矩形荒地ABCD(BC>AB)进行绿化和硬化,设计方案如图所示.矩形L、M、N为三块绿地.其余为硬化路面,L、M、N三块绿地周围的硬化路面宽都相等.并使三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$. 如图,菱形ABCD的周长为8,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO=1:2,菱形ABCD的面积S=$\frac{16}{5}$.
如图,菱形ABCD的周长为8,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO=1:2,菱形ABCD的面积S=$\frac{16}{5}$.