题目内容
19.已知点P(2,2)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,(1)求k的值;
(2)当1<x<3时,求y的取值范围.
分析 (1)由点P的坐标结合反比例函数图象上点的坐标特征即可得出结论;
(2)由(1)得知k=4,由k>0可知反比例函数图象在第一象限内单调递减,求出当x=1、x=3时y的值,根据单调性即可得出结论.
解答 解:(1)∵点P(2,2)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,
∴k=2×2=4.
(2)∵k=4>0,
∴反比例函数y=$\frac{4}{x}$在第一象限内单调递减.
∵当x=1时,y=$\frac{4}{1}$=4;当x=3时,y=$\frac{4}{3}$.
∴$\frac{4}{3}$<y<4.
故当1<x<3时,y的取值范围为:$\frac{4}{3}$<y<4.
点评 本题考查了反比例函数图象上点的坐标特征以及反比例函数的性质,解题的关键是:(1)熟练的运用反比例函数图象上点的坐标特征解决问题;(2)由k的值找出反比例函数在图象所在的每个象限内的单调性.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数系数k的值,得出反比例函数在图象所在的每个象限内的单调性是关键.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | a3+a4=a7 | B. | (a3)4=a7 | C. | (-a2b3)3=a6b9 | D. | 2a4•3a5=6a9 |
14.|-5+3|=( )
| A. | -8 | B. | 8 | C. | -2 | D. | 2 |
9.济南市名校德润中学九年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了$\frac{1}{3}$小时后,其余学生乘汽车出发,结果他们同时达到,已知乘汽车学生的速度是骑车学生速度的2倍,求骑车学生的速度.设骑车学生的速度为每小时x千米,则所列方程正确的是( )
| A. | $\frac{10}{x}=\frac{10}{2x}+\frac{1}{3}$ | B. | $\frac{10}{2x}=\frac{10}{x}+\frac{1}{3}$ | C. | $\frac{10}{x}=\frac{1}{3}-\frac{10}{2x}$ | D. | $\frac{10}{2x}-\frac{1}{3}=\frac{10}{x}$ |
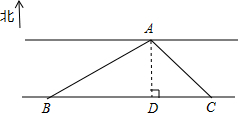 聪明的小亮运用数学知识帮爸爸测量河的宽度,测量过程如图所示,在河岸B点测得对岸一水站在北偏东60°的方向上,沿河岸行走300m到达C处,此时测得点A在北偏西45°方向上,你能根据这些数据帮小亮计算出河的宽度AD的值吗?写明你计算的过程.($\sqrt{2}≈1.4$,$\sqrt{3}≈1.7$,结果保留一位小数)
聪明的小亮运用数学知识帮爸爸测量河的宽度,测量过程如图所示,在河岸B点测得对岸一水站在北偏东60°的方向上,沿河岸行走300m到达C处,此时测得点A在北偏西45°方向上,你能根据这些数据帮小亮计算出河的宽度AD的值吗?写明你计算的过程.($\sqrt{2}≈1.4$,$\sqrt{3}≈1.7$,结果保留一位小数) 如图,DE∥BC,BE平分∠ABC,若∠ADE=60°,则∠1=30°.
如图,DE∥BC,BE平分∠ABC,若∠ADE=60°,则∠1=30°.