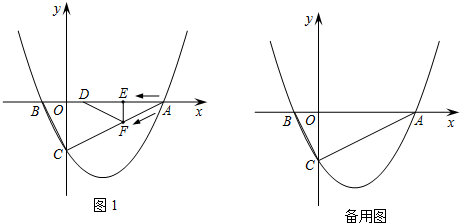题目内容
10.直线AB上有点O,作OC⊥CD,如果∠AOC=30°,那么∠BOD=60°或120°.分析 根据题意画出图形,根据垂线的性质可得∠COD=90°,然后再根据条件∠AOC=30°可得∠BOD的度数.
解答  解:如图1,∵OC⊥CD,
解:如图1,∵OC⊥CD,
∴∠COD=90°,
∵∠AOC=30°,
∴∠BOD=180°-30°-90°=60°;
如图2,∵OC⊥CD,
∴∠COD=90°,
∵∠AOC=30°,
∴∠AOD=90°-30°=60°,
∴∠BOD=180°-60°=120°,
故答案为:60°或120°.
点评 此题主要考查了垂线,关键是正确画出图形,分类计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15. 如图,在等边△ABC中,M,N分别在BC,AC上移动,且BM=CN,AM与BN相交于点Q,则∠BAM+∠ABN的度数是( )
如图,在等边△ABC中,M,N分别在BC,AC上移动,且BM=CN,AM与BN相交于点Q,则∠BAM+∠ABN的度数是( )
 如图,在等边△ABC中,M,N分别在BC,AC上移动,且BM=CN,AM与BN相交于点Q,则∠BAM+∠ABN的度数是( )
如图,在等边△ABC中,M,N分别在BC,AC上移动,且BM=CN,AM与BN相交于点Q,则∠BAM+∠ABN的度数是( )| A. | 60° | B. | 55° | C. | 45° | D. | 不能确定 |
19.下列说法中正确的是( )
| A. | 有一组邻边相等的梯形是等腰梯形 | |
| B. | 一组对边平行,另一组对边相等的四边形是等腰梯形 | |
| C. | 有一组对角互补的梯形是等腰梯形 | |
| D. | 有两组对角分别相等的四边形是等腰梯形 |
1.已知关于x的方程x2+bx+a=0有一个根是a(a≠0),则a+b的值为( )
| A. | 2 | B. | -1 | C. | 0 | D. | 1 |
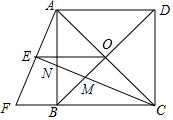 如图,正方形ABCD的对角线AC、BD相交于点O,延长CB至点F,使CF=CA,∠ACF的平分线分别交AF、AB、BD于点E、N、M,连接EO.
如图,正方形ABCD的对角线AC、BD相交于点O,延长CB至点F,使CF=CA,∠ACF的平分线分别交AF、AB、BD于点E、N、M,连接EO.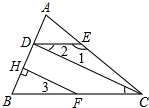 完成证明并写出推理根据:
完成证明并写出推理根据: 如图,AB和⊙O切于点B,AB=4,OB=2,则tanA=$\frac{1}{2}$.
如图,AB和⊙O切于点B,AB=4,OB=2,则tanA=$\frac{1}{2}$.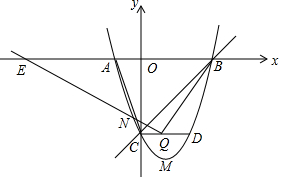 如图,已知抛物线与x轴交于A(-1,0),B(3,0),与y轴交于C(0,-3),顶点为点M.
如图,已知抛物线与x轴交于A(-1,0),B(3,0),与y轴交于C(0,-3),顶点为点M.