题目内容
18. 如图,AB和⊙O切于点B,AB=4,OB=2,则tanA=$\frac{1}{2}$.
如图,AB和⊙O切于点B,AB=4,OB=2,则tanA=$\frac{1}{2}$.
分析 先根据切线的性质得出∠AOB=90°,再由锐角三角函数的定义即可得出结论.
解答 解:∵AB和⊙O切于点B,
∴OB⊥AB.
∵AB=4,OB=2,
∴tanA=$\frac{OB}{AB}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查的是切线的性质,熟知圆的切线垂直于经过切点的半径是解答此题的关键.

练习册系列答案
相关题目

 如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.
如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O. 如图,△ABC为直角三角形,∠B=90°,AC边上取一点D,使CD=AB,分别过点C作CE⊥BC,过D作DE⊥AC,CE,DE相交于E.连结AE.
如图,△ABC为直角三角形,∠B=90°,AC边上取一点D,使CD=AB,分别过点C作CE⊥BC,过D作DE⊥AC,CE,DE相交于E.连结AE.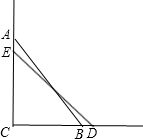 如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长25m,顶端A在AC上运动,量得滑杆下端B距C点的距离为15m,当端点B向右移动5m时到达D点,而A到达E点,求滑杆顶端A下滑多少米?
如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长25m,顶端A在AC上运动,量得滑杆下端B距C点的距离为15m,当端点B向右移动5m时到达D点,而A到达E点,求滑杆顶端A下滑多少米? 如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,AB=6,AC=4,若S△ABD=9,求S△ACD.
如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,AB=6,AC=4,若S△ABD=9,求S△ACD.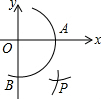 如图,在平面直角坐标系中,以点O为圆心,适当的长为半径画弧,交x轴于点A,交y轴于点B,再分别以点A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧在第四象限交于点P.若点P的坐标为(2a,a-9),则a的值为3.
如图,在平面直角坐标系中,以点O为圆心,适当的长为半径画弧,交x轴于点A,交y轴于点B,再分别以点A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧在第四象限交于点P.若点P的坐标为(2a,a-9),则a的值为3.