题目内容
5.如图1,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D,(1)判断BC与MD的位置关系,并说明理由;
(2)若AE=8,BE=2,求线段CD的长;
(3)如图2,若MD恰好经过圆心O,求∠D的度数.

分析 (1)BC与MD平行,理由为:在圆O中,利用同弧所对的圆周角相等得到一对角相等,再由已知角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行即可得证;
(2)连接OD,如图1所示,由AE+BE求出AB的长,即为圆的直径,求出半径OD的长,由AB垂直于CD,利用垂径定理及勾股定理求出DE的长,根据CD=2ED求出CD的长即可;
(3)连接MC,如图2所示,由AB为圆的直径,AB垂直于CD,利用垂径定理得到B为$\widehat{CD}$中点,再由已知角相等,利用圆周角定理得到∠CMB=∠BMD=∠D,由MD为直径,得到MC垂直于CD,利用直角三角形的性质确定出∠D的度数.
解答 解:(1)BC∥MD,理由为:
证明:∵在⊙O中,∠CBM=∠D,且∠M=∠D,
∴∠M=∠CBM,
∴BC∥MD;
(2)连结OD,如图1所示,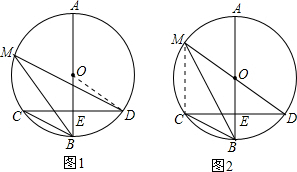 ∵AE=8,BE=2,
∵AE=8,BE=2,
∴直径AB=10,
∴OD=5,
∴OE=OB-BE=5-2=3,
又∵CD⊥AB,
∴DE=$\sqrt{O{D}^{2}-O{E}^{2}}$=4,
又∵AB为⊙O的直径,AB⊥CD,
∴CD=2DE=8;
(3)连结MC,如图2所示,
∵AB为⊙O的直径,AB⊥CD,
∴$\widehat{CB}$=$\widehat{BD}$,
∴∠CMB=∠BMD=∠D,
又∵MD过圆心,
∴∠MCD=90°,
∴∠D+∠CMB+∠BMD=90°,
∴∠D=30°.
点评 此题属于圆的综合题,涉及的知识有:平行线的判定,圆周角定理,垂径定理,勾股定理,熟练掌握定理及性质是解本题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
10.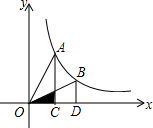 如图是一个反比例函数(x>0)的图象,点A(2,4)在图象上,AC⊥x轴于C,当点A运动到图象上的点B(4,2)处,BD⊥x轴于D,△AOC与△BOD重叠部分的面积为( )
如图是一个反比例函数(x>0)的图象,点A(2,4)在图象上,AC⊥x轴于C,当点A运动到图象上的点B(4,2)处,BD⊥x轴于D,△AOC与△BOD重叠部分的面积为( )
 如图是一个反比例函数(x>0)的图象,点A(2,4)在图象上,AC⊥x轴于C,当点A运动到图象上的点B(4,2)处,BD⊥x轴于D,△AOC与△BOD重叠部分的面积为( )
如图是一个反比例函数(x>0)的图象,点A(2,4)在图象上,AC⊥x轴于C,当点A运动到图象上的点B(4,2)处,BD⊥x轴于D,△AOC与△BOD重叠部分的面积为( )| A. | 1 | B. | 2 | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |

 已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P. 如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.