题目内容
13．一元二次方程2x2-3x+k=0有两个不相等的实数根，则k的最大整数值是1．分析 根据一元二次方程2x2-3x+k=0有两个不相等的实数根可得△=9-8k＞0，求出k的取值范围，进而得到k的最大整数值．
解答 解：∵一元二次方程2x2-3x+k=0有两个不相等的实数根，
∴△＞0，即9-8k＞0，
∴k＜$\frac{9}{8}$，
∴k的最大整数为1，
故答案为：1．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
习题精选系列答案
相关题目
1．下面的数中，与-2的和为0的是（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | 2 | D． | -2 |
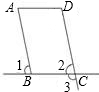如图，已知∠1=∠2，有下列结论：①∠3=∠D；②AB∥CD；③AD∥BC；④∠A+∠D=180°，其中正确的个数为（ ）
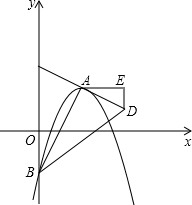如图，在平面直角坐标系xOy中，抛物线y=-$\frac{1}{4}$（x-m）2+$\frac{1}{4}$m2-m的顶点为A，与y轴的交点为B，连结AB，AC⊥AB，交y轴于点C，延长CA到点D，使AD=AC，连结BD．作AE∥x轴，DE∥y轴．