题目内容
18.记sn=a1+a2+…+an,令Tn=$\frac{{s}_{1}+{s}_{2}+…+{s}_{n}}{n}$,则称Tn为a1,a2,…,an这列数的“凯森和”.已知a1,a2,…,a500的“凯森和”为2004,那么13,a1,a2,…,a500的“凯森和”为( )| A. | 2013 | B. | 2015 | C. | 2017 | D. | 2019 |
分析 先根据已知求出T500的值,再设出新的凯森和Tx,列出式子,把得数代入,即可求出结果.
解答 解:∵Tn=$\frac{{S}_{1}+{S}_{2}+..+{S}_{n}}{n}$,
∴T500=2004,
设新的理想数为Tx,
501×Tx=13×501+500×T500,
Tx=(13×501+500×T500)÷501,
=$\frac{13×501+500×2004}{501}$,
=13+500×4
=2013.
故选:A.
点评 此题考查了数字的变化类,解题的关键是掌握“理想数”这个新概念,找出其中的规律,再根据新概念对要求的式子进行变形整理即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.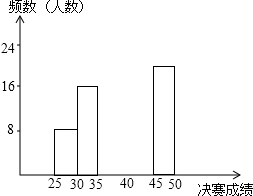 为增强学生的环保意识,某校组织学生开展了“雾霾天气知多少宣传暨竞赛活动”,经各班选拔,共推选出100名学会说呢过参加本次竞赛的决赛活动,决赛题设置了50道选择题,每答对一题得1分,满分50分,学校竞赛组委会经过统计,把这100名参赛学生的决赛成绩分成了5个组,并绘制出部分频数分布表和部分频数分布直方图如下:
为增强学生的环保意识,某校组织学生开展了“雾霾天气知多少宣传暨竞赛活动”,经各班选拔,共推选出100名学会说呢过参加本次竞赛的决赛活动,决赛题设置了50道选择题,每答对一题得1分,满分50分,学校竞赛组委会经过统计,把这100名参赛学生的决赛成绩分成了5个组,并绘制出部分频数分布表和部分频数分布直方图如下:
请结合图完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第1组8名同学中,有4名男同学,现将这8名同学平均分成两组参加学校环保宣传活动,4名男同学每组分2人,求小宇与小强两名男同学能分在同一组的概率.
 为增强学生的环保意识,某校组织学生开展了“雾霾天气知多少宣传暨竞赛活动”,经各班选拔,共推选出100名学会说呢过参加本次竞赛的决赛活动,决赛题设置了50道选择题,每答对一题得1分,满分50分,学校竞赛组委会经过统计,把这100名参赛学生的决赛成绩分成了5个组,并绘制出部分频数分布表和部分频数分布直方图如下:
为增强学生的环保意识,某校组织学生开展了“雾霾天气知多少宣传暨竞赛活动”,经各班选拔,共推选出100名学会说呢过参加本次竞赛的决赛活动,决赛题设置了50道选择题,每答对一题得1分,满分50分,学校竞赛组委会经过统计,把这100名参赛学生的决赛成绩分成了5个组,并绘制出部分频数分布表和部分频数分布直方图如下:| 组别 | 决赛成绩 x(分) | 频数(人数) |
| 第1组 | 25≤x<30 | 8 |
| 第2组 | 30≤x<35 | 16 |
| 第3组 | 35≤x<40 | 32 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 20 |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第1组8名同学中,有4名男同学,现将这8名同学平均分成两组参加学校环保宣传活动,4名男同学每组分2人,求小宇与小强两名男同学能分在同一组的概率.
 由几个大小相同的正方体组成的几何体如图所示,则它的俯视图为( )
由几个大小相同的正方体组成的几何体如图所示,则它的俯视图为( )



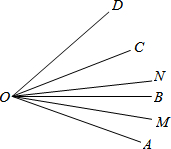 如图,OM平分∠AOB,ON平分∠COD,若∠MON=42°,∠BOC=5°,则∠AOD的度数是74°.
如图,OM平分∠AOB,ON平分∠COD,若∠MON=42°,∠BOC=5°,则∠AOD的度数是74°.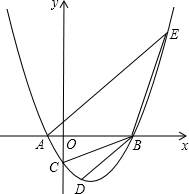 设抛物线y=ax2+bx-2与x轴交于两个不同的点A(一1,0)、B(4,0),与y轴交于点C.
设抛物线y=ax2+bx-2与x轴交于两个不同的点A(一1,0)、B(4,0),与y轴交于点C.