Question

18．如图，已知等边△ABC和点P，设点到△ABC三边AB、AC、BC（或其延长线）的距离分别为h₁、h₂、h₃，△ABC的高为h．
在图（1）中，点P是边BC的中点，此时h₃=0，可得结论：h₁+h₂+h₃=h．
在图（2）--（5）中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．
（1）请探究：图（2）--（5）中，h₁、h₂、h₃、h之间的关系；（直接写出结论）
（2）证明图（2）所得结论；
（3）证明图（4）所得结论．

Answer 1

分析 （1）根据已知可以证得：②h_l+h₂+h₃=h；③h₁-h₂+h₃=h；④h₁+h₂+h₃=h；⑤h₁+h₂-h₃=h；
（2）连接AP，可得S_△APB+S_△APC=S_△ABC，由h₃=0，AB=AC=BC，即可证得h₁+h₂+h₃=h；
（3）连接PA、PB、PC，可得S_△APB+S_△APC=S_△ABC+S_△BPC，由AB=AC=BC，即可求得h₁+h₂=h+h₃，则可得h₁+h₂-h₃=h．

解答 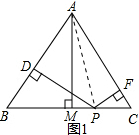解：（1）②h_l+h₂+h₃=h；③h₁-h₂+h₃=h；④h₁+h₂+h₃=h；⑤h₁+h₂-h₃=h．

（2）图1中，h₁+h₂+h₃=h．
连接AP，
则S_△APB+S_△APC=S_△ABC，
∴$\frac{1}{2}$AB×h₁+$\frac{1}{2}$AC×h₂=$\frac{1}{2}$BC×h．
又h₃=0，AB=AC=BC，
∴h₁+h₂+h₃=h．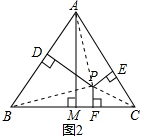

（3）图2中，h₁+h₂-h₃=h．
连接PA、PB、PC，（如答图）
则S_△APB+S_△APC=S_△ABC+S_△BPC．
∴$\frac{1}{2}$AB×h_l+$\frac{1}{2}$AC×h₂=$\frac{1}{2}$BC×h+$\frac{1}{2}$BC×h₃
又AB=AC=BC，
∴h₁+h₂=h+h₃．
∴h₁+h₂-h₃=h．

点评 本题考查的是三角形综合题．主要掌握等边三角形的性质，根据题意作出辅助线，构造出三角形，根据三角形的面积公式求解是解答此题的关键．