题目内容
16．计算：1+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+…+$\frac{1}{1+2+3+…+2014}$．分析 将原式变形为$\frac{1}{1}$+$\frac{1}{（1+2）×2÷2}$+$\frac{1}{（1+3）×3÷2}$+…+$\frac{1}{（1+2014）×2014÷2}$，进而变形为$\frac{2}{1×2}$+$\frac{2}{2×3}$+$\frac{2}{3×4}$+…+$\frac{2}{2014×2015}$，从而转化为2×（1-$\frac{1}{2015}$）求解．
解答 解：原式=$\frac{1}{1}$+$\frac{1}{（1+2）×2÷2}$+$\frac{1}{（1+3）×3÷2}$+…+$\frac{1}{（1+2014）×2014÷2}$
=$\frac{2}{2}$+$\frac{2}{3×2}$+$\frac{2}{4×3}$+…+$\frac{2}{2015×2014}$
=$\frac{2}{1×2}$+$\frac{2}{2×3}$+$\frac{2}{3×4}$+…+$\frac{2}{2014×2015}$
=2×（1-$\frac{1}{2015}$）
=$\frac{4028}{2015}$．
点评 本题考查了有理数的混合运算的知识，能够正确的变形是解答本题的关键，难度中等．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知：反比例函数y=$\frac{2}{x}$与一次函数交于点A，D，一次函数与x轴、y轴分别交于点C，B，求证：AB=CD．
甲车从A地出发，途径C地时休息一小时，然后按原速度继续前进到达B地；乙车从C地出发到B地后又按原速返回C地，两车同时出发，并以各自的速度匀速行驶，设A，C，B在同一条直线上，如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象．
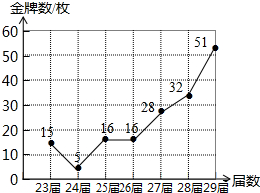从1984年起，我国先后参加了第23届夏季奥运会，取得了骄人的成绩．如图是根据第23届至29届夏季奥运会我国获得的金牌数绘制的折线统计图，观察统计图可得：与上一届相比增长量最大的是第29届夏季奥运会，比它的上一届增加了19枚金牌．
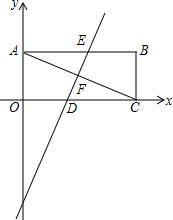如图，平面直角坐标系中，矩形OABC的两条邻边分别在x轴、y轴上，对角线AC=4$\sqrt{5}$，边OA=4．