题目内容
4.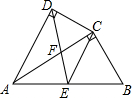 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.连接CE,连接DE交AC于F,AD=4,AB=6.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.连接CE,连接DE交AC于F,AD=4,AB=6.(1)求证:△ADC∽△ACB;
(2)求AC的值;
(3)求$\frac{AC}{AF}$的值.
分析 (1)根据两个角对应相等的两个三角形相似证明即可;
(2)根据相似三角形的对应边的比相等列出比例式,计算即可;
(3)根据直角三角形斜边上的中线是斜边的一半得到CE=AE,证明△AFD∽△CFE,根据相似三角形的性质解答即可.
解答 (1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB;
(2)解:∵△ADC∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$,即AC2=AD•AB=24,
解得,AC=2$\sqrt{6}$;
(3)解:∵E为AB的中点,
∴CE=$\frac{1}{2}$AB=AE,
∴∠EAC=∠ECA;
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
∴△AFD∽△CFE,
∴$\frac{AD}{CE}$=$\frac{AF}{CF}$,
∵CE=$\frac{1}{2}$AB=3,AD=4,
∴$\frac{AF}{CF}$=$\frac{4}{3}$,
∴$\frac{AC}{AF}$=$\frac{7}{4}$.
点评 本题考查的是直角三角形的性质、相似三角形的判定及其性质,牢固掌握直角三角形的性质、相似三角形的判定及其性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列说法中,错误的是( )
| A. | 三角形中至少有一个内角不小于60° | |
| B. | 三角形的角平分线、中线、高均在三角形的内部 | |
| C. | 有一个角是60°的等腰三角形是等边三角形 | |
| D. | 多边形的外角和等于360° |
12.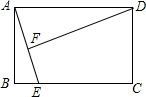 如图,矩形ABCD中,AB=3,AD=4,动点E从B点沿BC边移动到C停止,DF⊥AE于F,设E在运动过程中,AE长为x,DF长为y,则下列能反映y与x函数关系的是( )
如图,矩形ABCD中,AB=3,AD=4,动点E从B点沿BC边移动到C停止,DF⊥AE于F,设E在运动过程中,AE长为x,DF长为y,则下列能反映y与x函数关系的是( )
 如图,矩形ABCD中,AB=3,AD=4,动点E从B点沿BC边移动到C停止,DF⊥AE于F,设E在运动过程中,AE长为x,DF长为y,则下列能反映y与x函数关系的是( )
如图,矩形ABCD中,AB=3,AD=4,动点E从B点沿BC边移动到C停止,DF⊥AE于F,设E在运动过程中,AE长为x,DF长为y,则下列能反映y与x函数关系的是( )| A. | y=7x | B. | y=$\frac{12}{x}$ | C. | y=$\frac{12}{x}(3≤x≤5)$ | D. | y=$\frac{6}{x}$ |
9.下列说法正确的是( )
| A. | 线段AB和线段BA表示的不是同一条线段 | |
| B. | 射线AB和射线BA表示的是同一条射线 | |
| C. | 若点P是线段AB的中点,则PA=$\frac{1}{2}$AB | |
| D. | 线段AB叫做A、B两点间的距离 |
 已知一次函数的图象过如图两点.
已知一次函数的图象过如图两点.