题目内容
2．在等腰三角形ABC中，AB=AC，∠A=45°，BC=6，求它的腰长和底角．分析 利用等腰三角形的性质和三角形内角和定理可求得底角，过A作底边上的高，再结合三角函数可求得腰长．
解答 
解：∵AB=AC，∠A=45°，
∴∠ABC=∠ACB=$\frac{180°-45°}{2}$=67.5°，
过A作AD⊥BC，交BC于点D，
∵BC=6，
∴DC=$\frac{1}{2}$BC=3，
∴AB=AC=$\frac{3}{cos67.5°}$≈7.8．
点评 本题主要考查等腰三角形的性质，掌握等腰三角形的两底角相等是解题的关键，注意三线合一性质的利用．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
12．
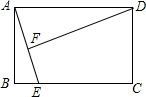如图，矩形ABCD中，AB=3，AD=4，动点E从B点沿BC边移动到C停止，DF⊥AE于F，设E在运动过程中，AE长为x，DF长为y，则下列能反映y与x函数关系的是（ ）
如图，矩形ABCD中，AB=3，AD=4，动点E从B点沿BC边移动到C停止，DF⊥AE于F，设E在运动过程中，AE长为x，DF长为y，则下列能反映y与x函数关系的是（ ）| A． | y=7x | B． | y=$\frac{12}{x}$ | C． | y=$\frac{12}{x}（3≤x≤5）$ | D． | y=$\frac{6}{x}$ |
如图，抛物线y1=-$\frac{1}{2}$x2+bx+c经过点A（4，0）和B（1，0），与y轴交于点C．