题目内容
12. 如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E.(1)求证:AC是⊙O的切线;
(2)若AB=9,sin∠BAC=$\frac{2}{3}$,求BE的长.
分析 (1)连接OD,由圆的性质得OB=OD,再由角平分线的性质得出OD∥BC,由垂直的定义得BC⊥AC,即可得出AC是⊙O的切线;
(2)根据三角函数的定义得出sin∠BAC=$\frac{2}{3}$,再由相似的定义得出△AOD∽△ABC,即可得出半径,过O作OF⊥BC于点F,则OF∥AC,由垂径定理得BE即可.
解答 证明: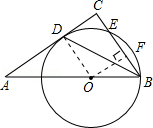 (1)如图,连接OD,
(1)如图,连接OD,
∵⊙O经过B,D两点,
∴OB=OD,
∴∠OBD=∠ODB,
又∵BD是∠ABC的平分线,
∴∠OBD=∠CBD.
∴∠ODB=∠CBD,
∴OD∥BC,
∵∠ACB=90°,即BC⊥AC,
∴OD⊥AC,
又∵OD是⊙O的半径,
∴AC是⊙O的切线.
(2)设⊙O的半径为R,在Et△ABC中,∠ACB=90°,
∵AB=9,sin∠BAC=$\frac{BC}{AB}$=$\frac{2}{3}$,
∴BC=$\frac{2}{3}$×9=6
∵OD∥BC,
∴△AOD∽△ABC,
∴$\frac{OD}{BC}$=$\frac{OA}{AB}$,即$\frac{R}{6}$=$\frac{9-R}{9}$,
解得:R=3.6
过O作OF⊥BC于点F,则OF∥AC,
∴∠BOF=∠BAC,
∴$\frac{BF}{OB}$=sin∠BOF=$\frac{2}{3}$,
∴BF=$\frac{2}{3}$×3.6=2.4
∴由垂径定理得:BE=2BF=2×2.4=4.8.
点评 本题考查了切线的判定以及相似三角形的判定和性质,是一道综合性的题目,把切线的判定、垂径定理以及三角函数的定义相结合,是中考的常见题型.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
20. 如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
 如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )| A. | π | B. | 2π | C. | $\frac{π}{2}$ | D. | 4π |
7.为了解某社区居民的用电情况,某数学活动小组随机对该社区20户居民进行了调查,下表是这20户居民某月用电量的调查结果:
则这20户居民该月用电量的中位数是110千瓦时,平均数是105千瓦时.
| 月用电量(千瓦时) | 60 | 80 | 100 | 120 | 140 |
| 户数(户) | 2 | 3 | 5 | 8 | 2 |
4.下列图形中,既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.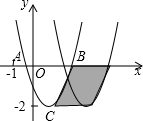 如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是( )
如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是( )
 如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是( )
如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是( )| A. | b>0 | B. | a-b+c<0 | ||
| C. | 阴影部分的面积为4 | D. | 若c=1,则b2=-4a |