��Ŀ����
��ͼ��������y=-x2+2x+3��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪD��

��1��ֱ��д��A��B��C���������������ߵĶԳ��
��2������BC���������ߵĶԳ��ύ�ڵ�E����PΪ�߶�BC�ϵ�һ�����㣬����P��PF��DE���������ڵ�F�����P�ĺ�����Ϊm��
���ú�m�Ĵ���ʽ��ʾ�߶�PF�ij����������mΪ��ֵʱ���ı���PEDFΪƽ���ı��Σ�
�����BCF�����ΪS����S��m�ĺ�����ϵ��
��3�������������£��ı���PEDF�����ǵ���������������ܣ�ֱ��д��m��ֵ����������ܣ���˵�����ɣ�

��1��ֱ��д��A��B��C���������������ߵĶԳ��
��2������BC���������ߵĶԳ��ύ�ڵ�E����PΪ�߶�BC�ϵ�һ�����㣬����P��PF��DE���������ڵ�F�����P�ĺ�����Ϊm��
���ú�m�Ĵ���ʽ��ʾ�߶�PF�ij����������mΪ��ֵʱ���ı���PEDFΪƽ���ı��Σ�
�����BCF�����ΪS����S��m�ĺ�����ϵ��
��3�������������£��ı���PEDF�����ǵ���������������ܣ�ֱ��д��m��ֵ����������ܣ���˵�����ɣ�
���㣺���κ����ۺ���
ר�⣺
��������1����֪�������ߵĽ���ʽ����y=0ʱ�����A��B��������꣬��x=0ʱ�������C������꣮���ݶԳ���x=-
�ɵó��Գ���Ľ���ʽ��
��2����PF�ij����ǵ�x=mʱ�������ߵ�ֵ��ֱ��BC����һ�κ�����ֵ�IJ���ȸ���B��C���������BC����ֱ�ߵĽ���ʽ��Ȼ��m�ֱ����ֱ��BC�������ߵĽ���ʽ�У���ó���������ֵ�IJ����PF�ij���
����ֱ��BC�Ľ���ʽ���ɵó�E������꣬���������ߵĽ���ʽ�����D������꣬Ȼ���������ϵ������ľ��빫ʽ�������DE�ij���Ȼ����PF=DE�����������ʱm��ֵ��
�ڿɽ�������BCF�ֳ�����������
һ������������PFC����PFΪ�ױߣ���P�ĺ�����Ϊ���ɵó�������PFC�������
һ������������PFB����PFΪ�ױߣ���P��B����ĺ������ľ���ֵΪ�ߣ��������������PFB�������
Ȼ�����������BCF�����=������PFC�����+������PFB����������������S��m�ĺ�����ϵʽ��
��3���ѡ�BCF�ָ�Ϊ��������FP�������Σ��ߵĺ͵���OB��
| b |
| 2a |
��2����PF�ij����ǵ�x=mʱ�������ߵ�ֵ��ֱ��BC����һ�κ�����ֵ�IJ���ȸ���B��C���������BC����ֱ�ߵĽ���ʽ��Ȼ��m�ֱ����ֱ��BC�������ߵĽ���ʽ�У���ó���������ֵ�IJ����PF�ij���
����ֱ��BC�Ľ���ʽ���ɵó�E������꣬���������ߵĽ���ʽ�����D������꣬Ȼ���������ϵ������ľ��빫ʽ�������DE�ij���Ȼ����PF=DE�����������ʱm��ֵ��
�ڿɽ�������BCF�ֳ�����������
һ������������PFC����PFΪ�ױߣ���P�ĺ�����Ϊ���ɵó�������PFC�������
һ������������PFB����PFΪ�ױߣ���P��B����ĺ������ľ���ֵΪ�ߣ��������������PFB�������
Ȼ�����������BCF�����=������PFC�����+������PFB����������������S��m�ĺ�����ϵʽ��
��3���ѡ�BCF�ָ�Ϊ��������FP�������Σ��ߵĺ͵���OB��
��� �⣺��1����y=0����-x2+2x+3=-��x+1����x-3��=0��
�⣺��1����y=0����-x2+2x+3=-��x+1����x-3��=0��
��ã�x=-1��x=3����A��-1��0����B��3��0����
���ԣ��Գ�����x=
=1��
��x=0����y=0����C��0��3����
����������A��-1��0����B��3��0����C��0��3���������ߵĶԳ�����x=1��
��2������ֱ��BC�ĺ�����ϵʽΪ��y=kx+b��k��0����
��B��3��0����C��0��3���ֱ����ã�
��
��ã�k=-1��b=3��
����ֱ��BC�ĺ�����ϵʽΪ��y=-x+3��
��x=1ʱ��y=-1+3=2��
��E��1��2����
��x=mʱ��y=-m+3��
��P��m��-m+3����
��y=-x2+2x+3�У���x=1ʱ��y=4��
��D��1��4��
��x=mʱ��y=-m2+2m+3��
��F��m��-m2+2m+3��
���߶�DE=4-2=2��
�߶�PF=-m2+2m+3-��-m+3��=-m2+3m
 ��PF��DE��
��PF��DE��
�൱PF=EDʱ���ı���PEDFΪƽ���ı��Σ�
��-m2+3m=2����ã�m1=2��m2=1���������⣬��ȥ����
��ˣ���m=2ʱ���ı���PEDFΪƽ���ı��Σ�
����ֱ��PF��x�ύ�ڵ�M����B��3��0����O��0��0�����ɵã�OB=OM+MB=3��
S=S��BCF=S��BPF+S��CPF=
FP•OM+
FP•BM=
(-m2+3m)��3=-
m2+
m��
m�ı仯��Χ��0��m��3��
��3����ͼ�ۣ�����ı���PEDF�ǵ������Σ���ôDG=EH�����yD-yF=yP-yE��
����4-��-m2+2m+3��=��-m+3��-2��
���m1=0�����CE�غϣ���ȥ����m2=1�����E�غϣ���ȥ����
����ı���PEDF�����ܳ�Ϊ�������Σ�
 �⣺��1����y=0����-x2+2x+3=-��x+1����x-3��=0��
�⣺��1����y=0����-x2+2x+3=-��x+1����x-3��=0����ã�x=-1��x=3����A��-1��0����B��3��0����
���ԣ��Գ�����x=
| 3-1 |
| 2 |
��x=0����y=0����C��0��3����
����������A��-1��0����B��3��0����C��0��3���������ߵĶԳ�����x=1��
��2������ֱ��BC�ĺ�����ϵʽΪ��y=kx+b��k��0����
��B��3��0����C��0��3���ֱ����ã�
|
��ã�k=-1��b=3��
����ֱ��BC�ĺ�����ϵʽΪ��y=-x+3��
��x=1ʱ��y=-1+3=2��

��E��1��2����
��x=mʱ��y=-m+3��
��P��m��-m+3����
��y=-x2+2x+3�У���x=1ʱ��y=4��
��D��1��4��
��x=mʱ��y=-m2+2m+3��
��F��m��-m2+2m+3��
���߶�DE=4-2=2��
�߶�PF=-m2+2m+3-��-m+3��=-m2+3m
 ��PF��DE��
��PF��DE���൱PF=EDʱ���ı���PEDFΪƽ���ı��Σ�
��-m2+3m=2����ã�m1=2��m2=1���������⣬��ȥ����
��ˣ���m=2ʱ���ı���PEDFΪƽ���ı��Σ�
����ֱ��PF��x�ύ�ڵ�M����B��3��0����O��0��0�����ɵã�OB=OM+MB=3��
S=S��BCF=S��BPF+S��CPF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
m�ı仯��Χ��0��m��3��
��3����ͼ�ۣ�����ı���PEDF�ǵ������Σ���ôDG=EH�����yD-yF=yP-yE��
����4-��-m2+2m+3��=��-m+3��-2��
���m1=0�����CE�غϣ���ȥ����m2=1�����E�غϣ���ȥ����
����ı���PEDF�����ܳ�Ϊ�������Σ�
������������Ҫ�����˶��κ������ۺ�Ӧ�ã����ݶ��κ����ó���ص������ͶԳ���Ľ���ʽ�ǽ���Ļ�����

��ϰ��ϵ�д�
�����Ŀ
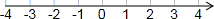 ��֪��ֽ������һ���ᣨ��ͼ�����۵�ֽ�森���磺����������2��ʾ�ĵ�����-2��ʾ�ĵ��غϣ�����������-4��ʾ�ĵ�����4��ʾ�ĵ��غϣ����������������⣬����������⣺
��֪��ֽ������һ���ᣨ��ͼ�����۵�ֽ�森���磺����������2��ʾ�ĵ�����-2��ʾ�ĵ��غϣ�����������-4��ʾ�ĵ�����4��ʾ�ĵ��غϣ����������������⣬����������⣺