题目内容
4. 如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点,连结AC.
如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点,连结AC.求证:(1)∠P=∠BAC
(2)直线CD是⊙O的切线.
分析 (1)要证明∠P=∠BAC,只要证明∠CAP+∠BAC=∠P+∠CAP即可,根据题目中的条件可以证明它们相等,从而可以解答本题;
(2)要证明直线CD是⊙O的切线,只要证明∠OCD=90°即可,根据题目中的条件和(1)中的结论可以证明∠OCD=90°,从而可以解答本题.
解答 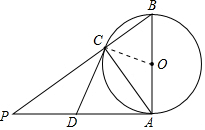 证明:(1)∵AB是⊙O的直径,
证明:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACP=90°,
∴∠P+∠CAP=90°,
∵AP⊙O是切线,
∴∠BAP=90°,
即∠CAP+∠BAC=90°
∴∠P=∠BAC;
(2)∵CD是Rt△PAC斜边PA的中线,
∴CD=AD,
∴∠DCA=∠DAC,
连接OC,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠DCO=∠DAO=90°,
∴CD是⊙O的切线.
点评 本题考查切线的判定与性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
14. 菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
 菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )| A. | (4,1) | B. | (4,-1) | C. | (1,4) | D. | (1,-4) |
19.下列各数中,是有理数的是( )
| A. | $\sqrt{0.9}$ | B. | -$\sqrt{3}$ | C. | π | D. | $\frac{1}{3}$ |
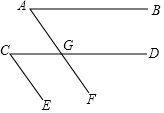 已知,如图:AB∥CD,若∠A的度数是x度,∠C的度数是y度,且x,y满足x2+y2=2xy,CE∥AF吗?为什么?
已知,如图:AB∥CD,若∠A的度数是x度,∠C的度数是y度,且x,y满足x2+y2=2xy,CE∥AF吗?为什么?
 如图,△ABC为直角三角形,∠B=90°,AC边上取一点D,使CD=AB,分别过点C作CE⊥BC,过D作DE⊥AC,CE,DE相交于E.连结AE.
如图,△ABC为直角三角形,∠B=90°,AC边上取一点D,使CD=AB,分别过点C作CE⊥BC,过D作DE⊥AC,CE,DE相交于E.连结AE.