题目内容
14.已知一次函数y=kx+2k+3的图象不经过第三象限,则k的取值范围为-$\frac{3}{2}$≤k<0.分析 由一次函数图象不过第三象限,利用一次函数图象与系数的关系即可得出关于k的一元一次不等式组,解之即可得出结论.
解答 解:∵一次函数y=kx+2k+3的图象不经过第三象限,
∴$\left\{\begin{array}{l}{k<0}\\{2k+3≥0}\end{array}\right.$,
解得:-$\frac{3}{2}$≤k<0.
故答案为:-$\frac{3}{2}$≤k<0.
点评 本题考查了一次函数图象与系数的关系,根据函数图象不过第三象限,找出关于k的一元一次不等式组是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
19.下列说法中正确的是( )
| A. | 有一组邻边相等的梯形是等腰梯形 | |
| B. | 一组对边平行,另一组对边相等的四边形是等腰梯形 | |
| C. | 有一组对角互补的梯形是等腰梯形 | |
| D. | 有两组对角分别相等的四边形是等腰梯形 |
6.计算代数式(a3b2)4的结果是( )
| A. | a7b6 | B. | a7b | C. | a3b2 | D. | a12b8 |
 如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点,连结AC.
如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点,连结AC.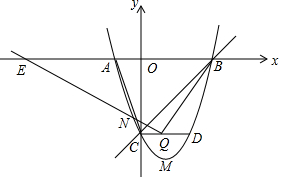 如图,已知抛物线与x轴交于A(-1,0),B(3,0),与y轴交于C(0,-3),顶点为点M.
如图,已知抛物线与x轴交于A(-1,0),B(3,0),与y轴交于C(0,-3),顶点为点M.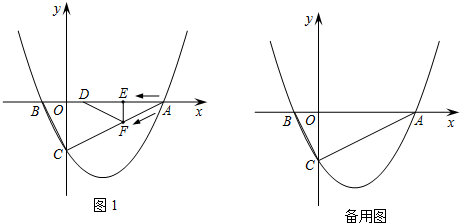
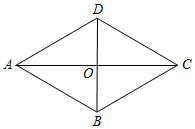 如图,菱形ABCD的面积为96,对角线AC=16,求这个菱形的周长.
如图,菱形ABCD的面积为96,对角线AC=16,求这个菱形的周长.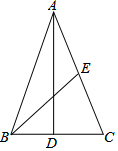 已知,如图△ABC中,AB=AC,AD⊥BC,BE是腰AC的中线,AD=12,BE=7.5,则△ABC的面积是36.
已知,如图△ABC中,AB=AC,AD⊥BC,BE是腰AC的中线,AD=12,BE=7.5,则△ABC的面积是36.