题目内容
若关于x的一元二次方程ax2+bx+c=0有两个实根x1、x2，分别满足条件：0＜x1＜1，1＜x2＜2，抛物线y=ax2+bx+c经过点（0，-2），有下列四个结论：①a+b＞2；②2a+b＜2；③a＜-1；④3a+b＞0，其中正确结论的个数为 ．
考点：二次函数图象与系数的关系
专题：
分析：由关于x的一元二次方程ax2+bx+c=0有两个实根x1、x2，分别满足条件：0＜x1＜1，1＜x2＜2，且抛物线y=ax2+bx+c经过点（0，-2），画出二次函数y=ax2+bx+c的草图，将（0，-2）代入y=ax2+bx+c，得出c=-2，那么y=ax2+bx-2．由x=1时，y＞0，可得a+b-2＞0，进而判断①正确；由x=2时，y＜0，可得4a+2b-2＜0，根据不等式的性质得到2a+b＜1，进而判断②正确；由a+b＞2，两边同乘-1，得-a-b＜-2，又2a+b＜1，两式相加得a＜-1，即可判断③正确；由0＜x1＜1，1＜x2＜2，根据不等式的性质得到
＜
，而
=-
，那么-
＜
，又a＜0，两边同乘-2a，得到b＜-3a，进而判断④错误．
| x1+x2 |
| 2 |
| 3 |
| 2 |
| x1+x2 |
| 2 |
| b |
| 2a |
| b |
| 2a |
| 3 |
| 2 |
解答：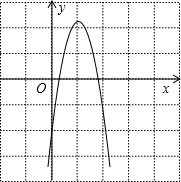
解：如图，∵抛物线y=ax2+bx+c经过点（0，-2），
∴c=-2，
∴y=ax2+bx-2．
①∵x=1时，y＞0，
∴a+b-2＞0，
∴a+b＞2，故①正确；
②∵x=2时，y＜0，
∴4a+2b-2＜0，
∴2a+b＜1，
∵1＜2，
∴2a+b＜2，故②正确；
③∵a+b＞2，
∴-a-b＜-2，
∵2a+b＜1，
两式相加得a＜-1，故③正确；
④∵0＜x1＜1，1＜x2＜2，
∴
＜
，
∵
=-
，
∴-
＜
，
∵a＜0，
∴b＜-3a，
∴3a+b＜0，故④错误．
所以正确结论的个数为3个．
故答案为3个．
解：如图，∵抛物线y=ax2+bx+c经过点（0，-2），∴c=-2，
∴y=ax2+bx-2．
①∵x=1时，y＞0，
∴a+b-2＞0，
∴a+b＞2，故①正确；
②∵x=2时，y＜0，
∴4a+2b-2＜0，
∴2a+b＜1，
∵1＜2，
∴2a+b＜2，故②正确；
③∵a+b＞2，
∴-a-b＜-2，
∵2a+b＜1，
两式相加得a＜-1，故③正确；
④∵0＜x1＜1，1＜x2＜2，
∴
| x1+x2 |
| 2 |
| 3 |
| 2 |
∵
| x1+x2 |
| 2 |
| b |
| 2a |
∴-
| b |
| 2a |
| 3 |
| 2 |
∵a＜0，
∴b＜-3a，
∴3a+b＜0，故④错误．
所以正确结论的个数为3个．
故答案为3个．
点评：本题考查了二次函数图象与系数的关系，二次函数与一元二次方程的关系，二次函数的性质，不等式的性质，难度适中．根据条件画出二次函数y=ax2+bx+c的草图，利用数形结合思想是解题的关键．
练习册系列答案
相关题目
如图，OA=2，OB=4，∠AOB=90°，点C为直线AB上一动点，以BC为腰作等腰直角三角形△BCE，过A、C、E三点作⊙O1，EF⊥BE交⊙O1于F点．
如图，在Rt△ABC中，∠BAC=90°，∠BAC的平分线交BC于点O，以O为圆心做圆，⊙O与AC相切于点D．在平面直角坐标系中，已知A（-1，-1）、B（2，3），若要在x轴上找一点P，使AP+BP最短，则点P的坐标为（ ）
| A、（0，0） | ||
B、（-
| ||
| C、（-1，0） | ||
D、（-
|
已知A（n，-2），B（1，4）是一次函数 y=kx+b的图象和反比例函数y=
如图，∠AOB=60°，∠AOC=90°，OB是∠AOD的平分线，求∠COD的度数．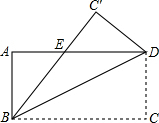
如图，将长方形ABCD沿BD对折，C点落在C′的位置，BC′与AD交于点E．