题目内容
2.在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(-y+2,x+2)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为-2<a<2,0<b<4.分析 根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,再写出点A1(a,b)的“伴随点”,然后根据x轴上方的点的纵坐标大于0列出不等式组求解即可.
解答 解:∵点A1的坐标为(a,b),
∴A2(-b+2,a+2),A3(-a,-b+4),A4(b-2,-a+2),A5(a,b),
…,
依此类推,每4个点为一个循环组依次循环,
∵对于任意的正整数n,点An均在x轴上方,
∴$\left\{\begin{array}{l}{a+2>0}\\{-a+2>0}\end{array}\right.$,$\left\{\begin{array}{l}{-b+4>0}\\{b>0}\end{array}\right.$,
解得-2<a<2,0<b<4.
故答案为:-2<a<2,0<b<4.
点评 本题是对点的变化规律的考查,读懂题目信息,理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键,也是本题的难点.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
13.若一个正多边形的每一个内角都等于120°,则它是( )
| A. | 正六边形 | B. | 正五边形 | C. | 正方形 | D. | 正八边形 |
17.若关于x的不等式组$\left\{\begin{array}{l}{x≥a}\\{\frac{x-1}{2}-\frac{2x-1}{6}<1}\end{array}\right.$的解集中只含有3个整数解,则a的取值范围是( )
| A. | -2<a≤-1 | B. | -2≤a<-1 | C. | 5<a≤6 | D. | 5≤a<6 |
7. 如图,在矩形ABCD中,对角线AC,BD相交于点O,且AD=6cm,CD=8cm,P是AB上的动点,PM⊥AC于M,PN⊥BD于N,则PM+PN的值为( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,且AD=6cm,CD=8cm,P是AB上的动点,PM⊥AC于M,PN⊥BD于N,则PM+PN的值为( )
 如图,在矩形ABCD中,对角线AC,BD相交于点O,且AD=6cm,CD=8cm,P是AB上的动点,PM⊥AC于M,PN⊥BD于N,则PM+PN的值为( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,且AD=6cm,CD=8cm,P是AB上的动点,PM⊥AC于M,PN⊥BD于N,则PM+PN的值为( )| A. | $\frac{24}{5}$cm | B. | 4cm | C. | 5cm | D. | $\frac{13}{5}$cm |
 如图,在平面直角坐标系中,四边形OABC为矩形,点A(0,8),C(6,0).动点P从点B出发,以每秒1个单位长的速度沿射线BC方向匀速运动,设运动时间为t秒.
如图,在平面直角坐标系中,四边形OABC为矩形,点A(0,8),C(6,0).动点P从点B出发,以每秒1个单位长的速度沿射线BC方向匀速运动,设运动时间为t秒. 如图,AB∥CD,点E在AB上,点F在CD上,连接EF,FG平分∠CFE交AB于点G,.若∠FEB=140°,求∠FGE的度数.
如图,AB∥CD,点E在AB上,点F在CD上,连接EF,FG平分∠CFE交AB于点G,.若∠FEB=140°,求∠FGE的度数.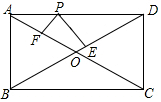 如图,矩形ABCD中,已知AD=4,AB=3,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,则PE+PF=( )
如图,矩形ABCD中,已知AD=4,AB=3,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,则PE+PF=( ) 在数轴上作出表示$\sqrt{20}$的点P(要求尺规作图,并保留痕迹).
在数轴上作出表示$\sqrt{20}$的点P(要求尺规作图,并保留痕迹). 如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,BD⊥OA,且OA•BD=$\frac{9}{2}$,则k的值为$\frac{3}{2}$.
如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,BD⊥OA,且OA•BD=$\frac{9}{2}$,则k的值为$\frac{3}{2}$.