题目内容
12. 如图,在平面直角坐标系中,四边形OABC为矩形,点A(0,8),C(6,0).动点P从点B出发,以每秒1个单位长的速度沿射线BC方向匀速运动,设运动时间为t秒.
如图,在平面直角坐标系中,四边形OABC为矩形,点A(0,8),C(6,0).动点P从点B出发,以每秒1个单位长的速度沿射线BC方向匀速运动,设运动时间为t秒.(1)当t=16s时,以OB、OP为邻边的平行四边形是菱形;
(2)当点P在OB的垂直平分线上时,求t的值;
(3)将△OBP沿直线OP翻折,使点B的对应点D恰好落在x轴上,求t的值.
分析 (1)先有菱形的性质得出PC=BC=8,进而得出BP=16即可得出结论;
(2)由线段的垂直平分线的性质得出PO=PB=t,再利用勾股定理即可求出结论;
(3)分点P在x轴坐标轴和负半轴上,利用勾股定理即可建立方程求解.
解答 解:(1)如图1,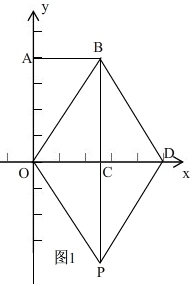
∵A(0,8),
∴OA=8,C(6,0),
∴OC=6,
∵四边形OABC是矩形,
∴BC=OA=8,
∵以OB、OP为邻边的平行四边形是菱形,
∴CP=BC=OA=8,
∴BP=BC+CP=16,
t=16÷1=16s,
故答案为16;
(2)如图2,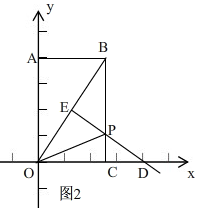 ∵点P是OB的垂直平分线上,
∵点P是OB的垂直平分线上,
∴PO=PB=t,
∴PC=BC-PB=8-t,
在Rt△POC中,OC=6,
根据勾股定理得,OC2+PC2=OP2,
∴62+(8-t)2=t2,
∴t=$\frac{25}{4}$,
(3)当点P在x轴的坐标轴上时,如图3,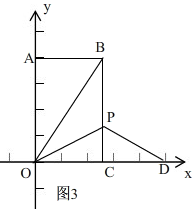
由折叠知,△OBP≌△ODP,
∴PD=PB=t,OD=OB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴CD=OD-OC=4,
在Rt△PCD中,CD=4,PC=BC-PB=8-t,PD=t,
根据勾股定理得,PC2+CD2=PD2,
∴42+(8-t)2=t2,
∴t=5,
当点P在x轴负半轴上时,如图4,
由折叠知,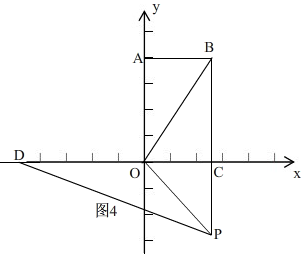 PB=PD=t,OD=OB=10,
PB=PD=t,OD=OB=10,
∴CD=OD+OC=16,PC=t-8,
在Rt△PCD中,根据勾股定理得,PC2+CD2=PD2,
∴(t-8)2+162=t2,
∴t=20,
即:满足条件的t的值为5s或20s.
点评 此题是一次函数综合题,主要考查了矩形的性质,菱形的性质,折叠的性质,勾股定理,垂直平分线定理,解(1)的关键是求出BP=2BC=16,解(2)的关键是利用线段的垂直平分线得出OP=PB,解(3)的关键是利用勾股定理建立方程求解,是一道常规题.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| A. | 2a和a2 | B. | -$\frac{1}{2}$ab和0.5ba | C. | a2b和ab2 | D. | 2和2a |
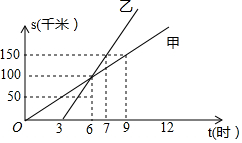 如图是甲、乙两人从同一地点出发后,路程s(千米)随时间t(时)变化的图象.
如图是甲、乙两人从同一地点出发后,路程s(千米)随时间t(时)变化的图象. 如图,AB∥CD,点P是AB、CD之间的点,∠BAP=$\frac{1}{5}$∠BAC,∠PCD=$\frac{1}{5}$∠DCA,过点P作直线EF交AB,CD于点E,F,此时∠APE+∠CPF=( )
如图,AB∥CD,点P是AB、CD之间的点,∠BAP=$\frac{1}{5}$∠BAC,∠PCD=$\frac{1}{5}$∠DCA,过点P作直线EF交AB,CD于点E,F,此时∠APE+∠CPF=( ) 如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C2017.若点P是第2016段抛物线的顶点,则P点的坐标为(-1,0).
如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C2017.若点P是第2016段抛物线的顶点,则P点的坐标为(-1,0). 如图,在四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,对角线AC=3,BD=2,则四边形EFGH的周长为( )
如图,在四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,对角线AC=3,BD=2,则四边形EFGH的周长为( )