题目内容
1. 小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.
小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.(1)小明行走的总路程是3800m,他途中休息了30min.
(2)①当60≤x≤90时,求y与x的函数关系式;②当小丽到达缆车终点时,小明离缆车终点的路程是多少?
分析 (1)由函数图象可以直接得出小明行走的路程是3800米,途中休息了30分钟;
(2)①设当60≤x≤90时,y与x的函数关系式为y=kx+b,由待定系数法求出其解即可;
②由路程÷速度=时间就可以得出小丽到达终点的时间,将这个时间代入(2)的解析式就可以求出小明行走的路程.
解答 解:(1)由函数图象,得
小亮行走的总路程是3800米,途中休息了60-30=30分钟.
故答案为:3800,30;
(2)①设当60≤x≤90时,y与x的函数关系式为y=kx+b,
∵图象过点(60,2000),(90,3800),
∴$\left\{\begin{array}{l}{60k+b=2000}\\{90k+b=3800}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=60}\\{b=-1600}\end{array}\right.$,
∴y=60x-1600;
②∵小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min,
∴小丽行驶的路程为;3800÷2=1900m,行驶的时间为:1900÷190=10min.
∴小丽到达终点,小明行驶的时间为:60+10=70min.
∴将x=70代入y=60x-1600得,y=60×70-1600=2600.
∴小明离缆车终点的路程是:3800-2600=1200m.
答:小明离缆车终点的路程是1200m.
点评 本题考查了一次函数的应用,时间=路程÷速度的运用,解答时由待定系数法求出一次函数的解析式是关键,认真分析函数图象的含义是重点.

练习册系列答案
相关题目
12.若分式$\frac{2}{a-1}$有意义,则a的取值范围是( )
| A. | a=0 | B. | a=1 | C. | a≠1 | D. | a≠-1 |
9.若点P关于x轴的对称点为P1(2a+b,3),关于y轴的对称点为P2(9,b+2),则点P的坐标为( )
| A. | (9,3) | B. | (-9,3) | C. | (9,-3) | D. | (-9,-3) |
16.某电视台组织知识竞赛,共设20道选择题,每题必答,如表记录了3个参赛者的得分情况.
(1)参赛者小婷得76分,她答对了几道题?
(2)参赛者小明说他得了80分.你认为可能吗?为什么?
(1)参赛者小婷得76分,她答对了几道题?
(2)参赛者小明说他得了80分.你认为可能吗?为什么?
| 参赛者 | 答对题数 | 答错题数 | 总得分 |
| 甲 | 20 | 0 | 100 |
| 乙 | 19 | 1 | 94 |
| 丙 | 14 | 6 | 64 |
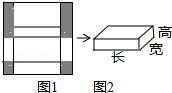 图1是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,这个长方体的高为5cm.
图1是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,这个长方体的高为5cm.