题目内容
7. 【问题提出】
【问题提出】对于特殊四边形,通常从定义、性质、判定、应用四个方面进行研究,我们借助于这种研究的过程与方法来研究一种新的四边形--筝形.
【定义】
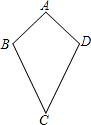
有且只有两组邻边分别相等的四边形称为筝形,如图,筝形ABCD是中,AB=AD,CB=CD且AB≠BC.
【性质】
按下列分类用文字语言填写相应的性质:
从对称性看:筝形是轴对称图形,它的对称轴是其中一条对角线所在直线.
从边看:有且只有两组邻边分别相等.
从对角线看:有且只有一条对角线被另一条对角线垂直平分.
【判定】
按要求用文字语言填写相应的判断方法,补全图形;
方法1:从边看,有且只有两组邻边分别相等的四边形.
方法2?从对角线看:有且只有一条对角线被另一条对角线垂直平分.
已知,如图,四边形ABCD中,AC垂直平分BD于O点,且AO≠CO.
求证:四边形ABCD是筝形.
证明:
【应用】
请利用筝形的定义、性质和判定解决以下问题.
(1)探索筝形ABCD的面积公式;
(2)筝形ABCD有外接圆吗?如果有,请作出他的对称轴;如果没有,请你在筝形ABCD中添加一个条件,使它有外接圆;
(3)筝形ABCD有内切圆吗?如果有,请作出它的内切圆,如果没有,请说明理由.
分析 【性质】根据图形及定义可以得出结论;【判定】结合图形与筝形的性质,可得出判定定理;【应用】(1)拆分筝形成两个三角形即可得出结论;(2)由直径所对的圆周角为90°能够找到缺失的条件--两个直角;(3)模拟三角形内切圆的画法的步骤即可得出结论.
解答 解:【性质】
结合判定的方法一和图形,即可得出结论:
从边看:有且只有两组邻边分别相等;从对角线看:有且只有一条对角线被另一条对角线垂直平分.
故答案为:两组对边都不平行;有且只有一条对角线被另一条对角线垂直平分.
【判定】
结合性质定理,可得出:方法二:从对角线看:有且只有一条对角线被另一条对角线垂直平分.
结合方法二可知缺少的条件为:AC垂直平分BD于O点,且AO≠CO.
故答案为:有且只有一条对角线被另一条对角线垂直平分;AC垂直平分BD于O点,且AO≠CO.
证明:按照题意,画出图形1.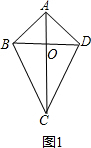
∵AC垂直平分BD,
∴AB=AD,CB=CD.
又∵AB=$\sqrt{A{O}^{2}+B{O}^{2}}$,BC=$\sqrt{B{O}^{2}+C{O}^{2}}$,AO≠CO,
∴AB≠BC,
∴由筝形定义得,四边形ABCD是筝形.
【应用】
(1)筝形面积为对角线乘积的一半;
∵SABCD=S△ABD+S△CBD=$\frac{1}{2}$BD•AO+$\frac{1}{2}$BD•CO=$\frac{1}{2}$BD(AO+CO)=$\frac{1}{2}$BD•AC,
∴筝形面积为对角线乘积的一半.
(2)不一定有,如果∠ABC=∠ADC=90°时,则有外接圆;
∵筝形只有一组对角相等,
∴∠ABC=∠ADC.
又∵AC>BD,
∴若筝形存在外接圆,其圆心为线段AC的中点,
∵B、D点在圆上,
∴∠ABC=∠ADC=90°.
故:不一定有,如果∠ABC=∠ADC=90°时,则有外接圆.
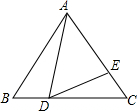
(3)有,作∠A和∠B的角平分线交于一点,过交点作AD的垂线,然后以交点为圆心,以垂线段为半径作圆,即为所求内切圆.
由筝形的性质可得出:$\left\{\begin{array}{l}{AB=AD}\\{BC=DC}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC,
∴∠BAC=∠DAC,∠BCA=∠DCA,
∴CA是∠BAD的角平分线.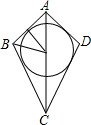
由AC为筝形对称轴可以得知存在内接圆.
点评 本题考查了新概念中的筝形的性质及判定,解题的关键是:读懂题意理清关系,用数学的语言合理的叙述.本题属于中档题型,难度不大,对应以前接触过筝形的同学来说本题不难,对于没接触过的同学来说有点难度,失分点是性质和判定定理的叙述,结合我们学过的知识,平行四边形、长方形和正方形的性质和判定定理,选用合适的数学语言来叙述是得分的关键,此处体现出了数学的严谨性.

 名校课堂系列答案
名校课堂系列答案| A. | 5x2y与-3xy2 | B. | 8xy2与-2x2z | C. | 10abc与-8ab | D. | 5ab与-5ba |
 (1)二次函数的图象经过点(4,-3),且当x=3时,函数有最大值-1,求此函数的解析式;
(1)二次函数的图象经过点(4,-3),且当x=3时,函数有最大值-1,求此函数的解析式;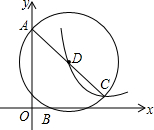 如图,平面直角坐标系中,已知A(0,3),B(1,0),点C在第一象限,⊙D经过点A、B、C三点,AC是⊙O的直径,双曲线y=$\frac{k}{x}$(x>0)经过D、C两点,则k的值是4.
如图,平面直角坐标系中,已知A(0,3),B(1,0),点C在第一象限,⊙D经过点A、B、C三点,AC是⊙O的直径,双曲线y=$\frac{k}{x}$(x>0)经过D、C两点,则k的值是4.