题目内容
对于函数y=k2x(k是常数,k≠0)的图象,下列说法不正确的是( )
| A、经过一、三象限或二、四象限$ | ||
B、过点(
| ||
| C、是一条直线 | ||
| D、y随着x的增大而增大 |
考点:正比例函数的性质
专题:
分析:根据正比例函数的性质求解.
解答:解:对于函数y=k2x(k是常数,k≠0)的图象,
∵k2>0,
∴直线y=k2x经过第一、三象限,y随x的增大而增大,
∵当x=
时,y=k,
∴直线y=k2x经过点(
,k).
故选A.
∵k2>0,
∴直线y=k2x经过第一、三象限,y随x的增大而增大,
∵当x=
| 1 |
| k |
∴直线y=k2x经过点(
| 1 |
| k |
故选A.
点评:BE题考查了正比例函数的性质:正比例函数y=kx(k≠0)的图象是直线,当k>0,经过第一、三象限,y随x的增大而增大;当k<0,经过第二、四象限,y随x的增大而减小.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
下列命题中正确的是( )
| A、无理数都是开方开不尽的数 |
| B、无理数包括正无理数,0,负无理数 |
| C、两个无理数之和一定是无理数 |
| D、无理数都可以用数轴上的点表示 |
 已知二次函数y=ax2+bx+c的图象如图,下列结论中,正确的结论的个数有( )
已知二次函数y=ax2+bx+c的图象如图,下列结论中,正确的结论的个数有( ) 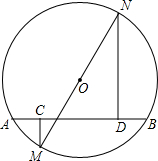 如图,⊙O的直径MN=20cm,弦AB=16cm,MC⊥AB于C,ND⊥AB于D.求ND-CM的值.
如图,⊙O的直径MN=20cm,弦AB=16cm,MC⊥AB于C,ND⊥AB于D.求ND-CM的值.