题目内容
8.某校为了解该校近1000名九年级学生第二次模拟考试的数学考试成绩的情况,从中随机抽取了100名学生的成绩进行统计,在这个问题中,以下说法:①这1000名学生的数学考试成绩是总体;
②个体是抽取的100名学生的数学考试成绩;
③每名学生的数学考试成绩是总体的一个样本;
④样本容量是100.
正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
解答 解:①这1000名学生的数学考试成绩是总体,故①正确;
②个体是1000名学生中每个学生的数学考试成绩,故②错误;
③抽取的100名学生的数学考试成绩是总体的一个样本,故③错误;
④样本容量是100,故④正确;
故选:B.
点评 本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
18.在密码学中,把直接可以看到的内容称为明码,对明码进行某种处理后得到的内容称为密码.有一种密码,将英文26个字母a,b,c,…z依次对应1、2、3,…,26这26个自然数,如下表,当明码对应的序号x为奇数时,密码对应的序号y=$\frac{x+1}{2}$;当明码对应的序号x为偶数时,密码对应的序号y=$\frac{x}{2}+13$.
按上述规定,将明码“love”译成密码(密码是字母)是s、h、x、c.
| 字母 | a | b | c | d | e | f | g | h | i | j | k | l | m |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 | n | o | p | q | r | s | t | u | v | w | x | y | z |
| 序号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
16.计算2$\sqrt{\frac{1}{2}}$$+3\sqrt{\frac{1}{3}}$$-\sqrt{8}$的结果是( )
| A. | $\sqrt{3}-\sqrt{2}$ | B. | $\sqrt{2}-\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3$\sqrt{2}$ |
20.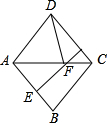 如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
 如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )| A. | 60° | B. | 50° | C. | 30° | D. | 20° |
17.若三角形两条边的长度分别是3cm和7cm,则第三条边的长度可能是( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 10cm |
18.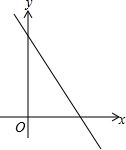 已知x关于的一次函数y=mx+n的图象如上图,则|n-m|-$\sqrt{m^2}+\sqrt{{{(m-n)}^2}}$可化简( )
已知x关于的一次函数y=mx+n的图象如上图,则|n-m|-$\sqrt{m^2}+\sqrt{{{(m-n)}^2}}$可化简( )
 已知x关于的一次函数y=mx+n的图象如上图,则|n-m|-$\sqrt{m^2}+\sqrt{{{(m-n)}^2}}$可化简( )
已知x关于的一次函数y=mx+n的图象如上图,则|n-m|-$\sqrt{m^2}+\sqrt{{{(m-n)}^2}}$可化简( )| A. | n | B. | n-2m | C. | m | D. | 2n-m |
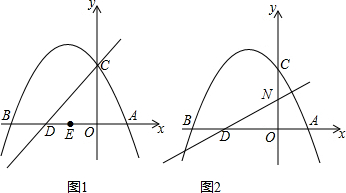
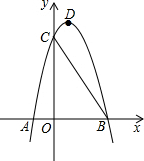 如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.
如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.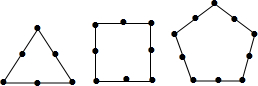 墨墨用黑色的棋子摆各种正多边形,如图所示,他摆正三角形的时候用了6个棋子,摆正方形的时候用了8个棋子,摆正五边形的时候用了10个棋子,以此类推,当墨墨摆完正十二边形时,共用了150个棋子.
墨墨用黑色的棋子摆各种正多边形,如图所示,他摆正三角形的时候用了6个棋子,摆正方形的时候用了8个棋子,摆正五边形的时候用了10个棋子,以此类推,当墨墨摆完正十二边形时,共用了150个棋子.