题目内容
13.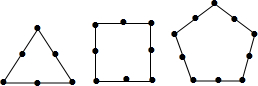 墨墨用黑色的棋子摆各种正多边形,如图所示,他摆正三角形的时候用了6个棋子,摆正方形的时候用了8个棋子,摆正五边形的时候用了10个棋子,以此类推,当墨墨摆完正十二边形时,共用了150个棋子.
墨墨用黑色的棋子摆各种正多边形,如图所示,他摆正三角形的时候用了6个棋子,摆正方形的时候用了8个棋子,摆正五边形的时候用了10个棋子,以此类推,当墨墨摆完正十二边形时,共用了150个棋子.
分析 观察图形,将顶点棋子算到同一个方向的边上,可以得出摆正n边形用了2n个棋子,将各图形棋子相加,即可得出结论.
解答 解:将顶点的棋子算到一侧(算逆时针边上),可知正三角形用了3×2个棋子,正方形用了4×2个棋子,正五边形用了5×2个棋子…,
由此可得知摆正n边形用了2n个棋子.
故当墨墨摆完正十二边形时,共用了3×2+4×2+…+12×2=(3+4+…+12)×2=10×$\frac{3+12}{2}$×2=150.
故答案为:150.
点评 本题考查了图形的变化,解题的关键是找出“摆正n边形用了2n个棋子”这一规律.本题属于中档题,难度不大,解决该类题型的方法是仔细观察图形,将顶点上的棋子算到同一侧的边上.

练习册系列答案
相关题目
2.等腰三角形的一个外角等于130°,则这个等腰三角形的底角为( )
| A. | 65° | B. | 50° | C. | 65°或40° | D. | 50°或65° |
 墨墨对他所住小区的100户居民2月份天然气的使用量(单位:m3)进行统计,其结果如图所示,图中36-38段因不小心洒上水而看不清,则2月份天然气的使用量在36-38段的居民有( )
墨墨对他所住小区的100户居民2月份天然气的使用量(单位:m3)进行统计,其结果如图所示,图中36-38段因不小心洒上水而看不清,则2月份天然气的使用量在36-38段的居民有( )