题目内容
等腰三角形的一边长为4，另两边长是关于x的方程x2-20x+m=0的两个实数根，则m的值为（ ）
| A、64 | B、100 |
| C、48 | D、64或100 |
考点：等腰三角形的性质,一元二次方程的解
专题：分类讨论
分析：由于一个等腰三角形的一边长为4，另两边长是关于x的方程x2-20x+m=0的两根，有两种情况：
①当腰长为4时，直接把x=4代入原方程即可求出m的值，然后求出方程的另一根，也就可以求出三角形的周长；
②当底边为4时，那么x的方程x2-20x+m=0的两根是相等的，利用判别式为0即可求出m的值，然后就可以求出方程的解，也就可以求出三角形的周长．
①当腰长为4时，直接把x=4代入原方程即可求出m的值，然后求出方程的另一根，也就可以求出三角形的周长；
②当底边为4时，那么x的方程x2-20x+m=0的两根是相等的，利用判别式为0即可求出m的值，然后就可以求出方程的解，也就可以求出三角形的周长．
解答：解：∵一个等腰三角形的一边长为4，另两边长是关于x的方程x2-20x+m=0的两根，
①当腰长为4时，把x=4代入原方程得
16-80+m=0，
∴m=64，
∴原方程变为：x2-20x+64=0，
设方程的另一个根为x，
则4+x=20，
∴x=16，
∵4+4＜16
∴不能构成三角形；
②当底边为4时，那么x的方程x2-20x+m=0的两根是相等的，
∴△=（-20）2-4m=0，
∴m=100，
∴方程变为x2-20x+100=0，
∴方程的两根相等为x1=x2=10，
∴三角形的周长为4+2×10=24．
综上，m的值是100，
故选B．
①当腰长为4时，把x=4代入原方程得
16-80+m=0，
∴m=64，
∴原方程变为：x2-20x+64=0，
设方程的另一个根为x，
则4+x=20，
∴x=16，
∵4+4＜16
∴不能构成三角形；
②当底边为4时，那么x的方程x2-20x+m=0的两根是相等的，
∴△=（-20）2-4m=0，
∴m=100，
∴方程变为x2-20x+100=0，
∴方程的两根相等为x1=x2=10，
∴三角形的周长为4+2×10=24．
综上，m的值是100，
故选B．
点评：此题主要考查了一元二次方程的解的定义和等腰三角形的性质，解题的关键是利用等腰三角形的性质得到方程的解，把方程的解代入原方程即可求出待定字母的取值即可解决问题．
练习册系列答案
相关题目
已知AD、AE分别为△ABC的角平分线、高线，若∠B=50°，∠C=60°，则∠ADB的度数为（ ）| A、75° | B、85° |
| C、95° | D、105° |
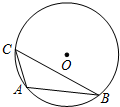如图，△ABC内接于⊙O，CB=a，CA=b，∠A-∠B=90°，则⊙O的半径为
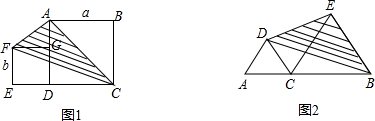在数学学习过程中，我们常常会有“似曾相识“的感觉，如果我们把这些类似进行比较、加以联想的话，可能出现许多意想不到的结果和方法，这种把类似进行比较、联想，从而解决问题的方法就是类比法，类比法是一种寻求解题思路，猜测问题答案或结论的发现方法．