题目内容
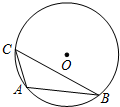 如图,△ABC内接于⊙O,CB=a,CA=b,∠A-∠B=90°,则⊙O的半径为
如图,△ABC内接于⊙O,CB=a,CA=b,∠A-∠B=90°,则⊙O的半径为考点:圆周角定理,勾股定理
专题:计算题
分析:作直径AE,连接BE,如图,根据圆周角定理得∠ACE=90°,∠AEC=∠ABC,易得∠ABC+∠CAE=90°,加上∠CAB-∠ABC=90°,则∠CAB+∠CAE=180°,所以∠DAC=∠CAE,根据圆内接四边形的性质和圆周角定理得∠DAC=∠BEC,∠CAE=∠CBE,所以∠CBE=∠CEB,则CE=CB=a,然后在Rt△ACE中根据勾股定理计算出AE,即可得到⊙O的半径.
解答:解:作直径AE,连接BE,如图,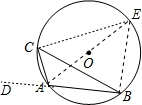 ∠DAC为△ABC的外角,
∠DAC为△ABC的外角,
∵AE为直径,
∴∠ACE=90°,
∴∠AEC+∠CAE=90°,
∵∠AEC=∠ABC,
∴∠ABC+∠CAE=90°,
∵∠CAB-∠ABC=90°,
∴∠CAB+∠CAE=180°,
而∠CAB+∠CAD=180°,
∴∠DAC=∠CAE,
∵∠DAC=∠BEC,∠CAE=∠CBE,
∴∠CBE=∠CEB,
∴CE=CB=a,
在Rt△ACE中,∵AC=b,CE=a,
∴AE=
=
,
∴⊙O的半径为
.
故答案为
.
 ∠DAC为△ABC的外角,
∠DAC为△ABC的外角,∵AE为直径,
∴∠ACE=90°,
∴∠AEC+∠CAE=90°,
∵∠AEC=∠ABC,
∴∠ABC+∠CAE=90°,
∵∠CAB-∠ABC=90°,
∴∠CAB+∠CAE=180°,
而∠CAB+∠CAD=180°,
∴∠DAC=∠CAE,
∵∠DAC=∠BEC,∠CAE=∠CBE,
∴∠CBE=∠CEB,
∴CE=CB=a,
在Rt△ACE中,∵AC=b,CE=a,
∴AE=
| AE2+AC2 |
| a2+b2 |
∴⊙O的半径为
| ||
| 2 |
故答案为
| ||
| 2 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了勾股定理.

练习册系列答案
相关题目
已知点(x1,y1)、(x2,y2)都在直线y=-
x+2上,若x1<x2,则y1,y2的大小关系是( )
| 1 |
| 2 |
| A、y1>y2 |
| B、y1=y2 |
| C、y1<y2 |
| D、不能比较 |
等腰三角形的一边长为4,另两边长是关于x的方程x2-20x+m=0的两个实数根,则m的值为( )
| A、64 | B、100 |
| C、48 | D、64或100 |
如果a与b互为相反数,x与y互为倒数,则代数式a+b-2xy的值为( )
| A、0 | B、-2 | C、-1 | D、无法确定 |
 如图是一个正方体的展开图,如果正方体相对两个面上的代数式的值相等,则x=
如图是一个正方体的展开图,如果正方体相对两个面上的代数式的值相等,则x=