题目内容
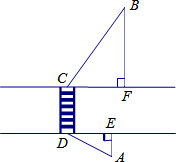 如图,从超市A到马路对面的车站B需走斑马线DC,已知马路宽CD=20米,超市A到马路边DE的距离AE=10米,车站B到马路边CF的距离BF=40米,且∠BCF=54°,∠ADE=30°.试求从超市A出发,沿A→D→C→B到车站共行走的路程.(结果精确到1米.参考数据:sin54°≈0.80,cos54°≈0.60,tan54°≈1.40)
如图,从超市A到马路对面的车站B需走斑马线DC,已知马路宽CD=20米,超市A到马路边DE的距离AE=10米,车站B到马路边CF的距离BF=40米,且∠BCF=54°,∠ADE=30°.试求从超市A出发,沿A→D→C→B到车站共行走的路程.(结果精确到1米.参考数据:sin54°≈0.80,cos54°≈0.60,tan54°≈1.40)考点:解直角三角形的应用
专题:
分析:在直角△ADE和直角△BCF中,利用三角函数求得BC和AD的长,则路程长即可求解.
解答:解:∵在直角△ADE中,sin∠ADE=
,
∴AD=
=2AE=20(米),
同理,在△BCF中,BC=
=
≈
=50(米),
则沿A→D→C→B到车站共行走的路程是:20+50+20=90(米).
答:沿A→D→C→B到车站共行走的路程是90米.
| AE |
| AD |
∴AD=
| AE |
| sin∠ADE |
同理,在△BCF中,BC=
| BF |
| sin∠BCF |
| 40 |
| sin54° |
| 40 |
| 0.80 |
则沿A→D→C→B到车站共行走的路程是:20+50+20=90(米).
答:沿A→D→C→B到车站共行走的路程是90米.
点评:本题考查了三角函数的应用,正确理解直角三角形的边角之间的关系是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据 tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据 tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).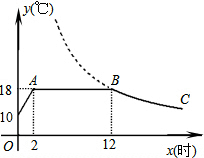 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.图中是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.图中是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y= 某商店第一次用600元购进某种铅笔若干支,第二次又用600元购进该种铅笔,但这次每支的进价比第一次贵1元,所以购进数量比第一次少了30支.
某商店第一次用600元购进某种铅笔若干支,第二次又用600元购进该种铅笔,但这次每支的进价比第一次贵1元,所以购进数量比第一次少了30支.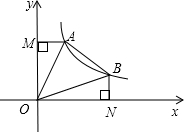 如图,直线y=-x+b(b>0)与双曲线y=
如图,直线y=-x+b(b>0)与双曲线y=