题目内容
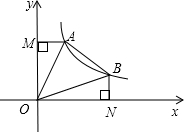 如图,直线y=-x+b(b>0)与双曲线y=
如图,直线y=-x+b(b>0)与双曲线y=| k |
| x |
①OA=OB;②△AOM≌△BON;③若∠AOB=45°,则S△AOB=k.
其中正确的是
考点:反比例函数综合题
专题:综合题
分析:①②设A(x1,y1),B(x2,y2),联立y=-x+b与y=
,得x2-bx+k=0,则x1•x2=k,又x1•y1=k,比较可知x2=y1,同理可得x1=y2,即ON=OM,AM=BN,可证结论;
③作OH⊥AB,垂足为H,根据对称性可证△OAM≌△OAH≌△OBH≌△OBN,可证S△AOB=k;
| k |
| x |
③作OH⊥AB,垂足为H,根据对称性可证△OAM≌△OAH≌△OBH≌△OBN,可证S△AOB=k;
解答: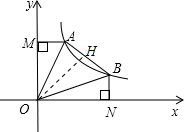 解:设A(x1,y1),B(x2,y2),代入y=
解:设A(x1,y1),B(x2,y2),代入y=
中,得x1•y1=x2•y2=k,
联立
,消去y得:x2-bx+k=0,
则x1•x2=k,又x1•y1=k,
∴x2=y1,
同理x2•y2=k,
可得x1=y2,
∴ON=OM,AM=BN,
在△AOM和△BON中,
∴△AOM≌△BON,
∴OA=OB,即①②正确;
③作OH⊥AB,垂足为H,
∵OA=OB,∠AOB=45°,
∵△AOM≌△BON,
∴∠MOA=∠BON=22.5°,∠AOH=∠BOH=22.5°,
∴△OAM≌△OAH≌△OBH≌△OBN,
∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON=
k+
k=k,正确;
正确的结论有①②③.
故答案为:①②③
 解:设A(x1,y1),B(x2,y2),代入y=
解:设A(x1,y1),B(x2,y2),代入y=| k |
| x |
联立
|
则x1•x2=k,又x1•y1=k,
∴x2=y1,
同理x2•y2=k,
可得x1=y2,
∴ON=OM,AM=BN,
在△AOM和△BON中,
|
∴△AOM≌△BON,
∴OA=OB,即①②正确;
③作OH⊥AB,垂足为H,
∵OA=OB,∠AOB=45°,
∵△AOM≌△BON,
∴∠MOA=∠BON=22.5°,∠AOH=∠BOH=22.5°,
∴△OAM≌△OAH≌△OBH≌△OBN,
∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON=
| 1 |
| 2 |
| 1 |
| 2 |
正确的结论有①②③.
故答案为:①②③
点评:此题考查了反比例函数的综合运用,解题的关键是明确反比例函数图象上点的坐标特点,反比例函数图象的对称性.

练习册系列答案
相关题目
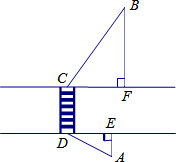 如图,从超市A到马路对面的车站B需走斑马线DC,已知马路宽CD=20米,超市A到马路边DE的距离AE=10米,车站B到马路边CF的距离BF=40米,且∠BCF=54°,∠ADE=30°.试求从超市A出发,沿A→D→C→B到车站共行走的路程.(结果精确到1米.参考数据:sin54°≈0.80,cos54°≈0.60,tan54°≈1.40)
如图,从超市A到马路对面的车站B需走斑马线DC,已知马路宽CD=20米,超市A到马路边DE的距离AE=10米,车站B到马路边CF的距离BF=40米,且∠BCF=54°,∠ADE=30°.试求从超市A出发,沿A→D→C→B到车站共行走的路程.(结果精确到1米.参考数据:sin54°≈0.80,cos54°≈0.60,tan54°≈1.40)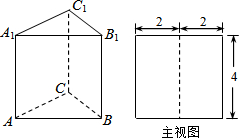 如图,直三棱柱ABC-A1B1C1的底面为正三角形,且主视图是边长为4的正方形,则此直三棱柱左视图的面积为
如图,直三棱柱ABC-A1B1C1的底面为正三角形,且主视图是边长为4的正方形,则此直三棱柱左视图的面积为 如图,圆锥的高h=4cm,底面半径r=3cm,则圆锥的全面积为
如图,圆锥的高h=4cm,底面半径r=3cm,则圆锥的全面积为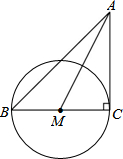 如图,在Rt△ABC中,∠C=90°,以BC为直径作⊙M,连结AM,若sin∠CAM=
如图,在Rt△ABC中,∠C=90°,以BC为直径作⊙M,连结AM,若sin∠CAM=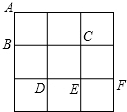 如图,在3×3方格纸中,点A、B、C、D、E、F分别位于小正方形的格点上.从A、D、
如图,在3×3方格纸中,点A、B、C、D、E、F分别位于小正方形的格点上.从A、D、